10. Проверка на простоту и факторизация

Решето Эратосфена

Решето Эратосфена - алгоритм, находящий все простые числа, не превосходящие некоторой границы $n$. Алгоритм рассматривает последовательно все числа от 2 до $n$. Если очередное число ещё не помечено как составное, он помечает его как простое, а все числа, делящиеся на него, помечает как составные.

Поскольку у любого составного числа $x$ есть делитель, не больший корня из $x$, достаточно перебирать кратные простого числа, начиная с его квадрата.

1
2
3
4
5
6


vector<bool> isPrime(n + 1, 1)
isPrime[0] = isPrime[1] = 0
for i = 2..n:
    if isPrime[i]:
        for (j = i * i; j <= n; j += i):
            isPrime[j] = 0

Время работы алгоритма есть

$$ \sum_{\substack{p \text {-простое, } \\ p \leqslant n}} \frac{n}{p}=n \cdot\left(\sum_{\substack{p-п р о с т о е, ~}}^{p \leqslant n}<~ \frac{1}{p}\right)=O(n \log \log n) $$

поскольку

$$ \sum_{\substack{p-\text { простое, } \\ p \leqslant n}} \frac{1}{p}=O(\log \log n) $$

(факт из теории чисел, который мы доказывать не будем).

Решето с линейным временем работы

Существует алгоритм со временем работы $O(n)$ (Gries, Misra, 1978), который устроен похожим образом, но помечает каждое составное число ровно один раз. Более того, для каждого числа, не большего $n$, он находит его наименьший простой делитель, что позволяет потом быстро факторизовать (разложить на простые множители) любое из чисел.

Обозначим наименьший простой делитель $x$ за $p[x]$. Алгоритм помечает составное число $x$ в тот момент, когда он рассматривает число $\frac{x}{p[x]}$. Заметим, что $p[x] \leqslant p\left[\frac{x}{p[x]}\right]$.

Чтобы сделать все такие пометки, достаточно, рассматривая число $y$, пометить все числа вида $y q$, где $q$ - простое, меньшее или равное $p[y]$.

1
2
3
4
5
6
7
8


vector<int> primes # список простых чисел
vector<int> d(n + 1, -1) # d[i] - номер p[i] в списке простых
for i = 2..n:
    if d[i] == -1:
        d[i] = sz(primes)
        primes.push_back(i)
    for (j = 0; j <= d[i] and i * primes[j] <= n; ++j):
        d[i * primes[j]] = j

Перебор делителей

Пусть теперь мы хотим проверить на простоту конкретное число $n$. Самый простой способ - это перебрать все числа, большие единицы, но меньшие $n$, и проверить, делится ли $n$ хоть на одно из них. На самом деле достаточно перебирать числа, не большие $\sqrt{n}$, поскольку у составного $n$ точно найдётся нетривиальный делитель не больше $\sqrt{n}$. Тем не менее, если $b$ - длина битовой записи $n$, такой алгоритм всё ещё будет иметь сложность, экспоненциально зависящую от $b$ : он совершит $\Omega(\sqrt{n})=\Omega\left(2^{b / 2}\right)=\Omega\left((\sqrt{2})^{b}\right)$ итераций.

В криптографии часто возникает потребность в больших простых числах. Соответственно, хочется иметь алгоритм, умеющий проверять число на простоту за время, полиномиально зависящее от длины числа.

Тест Ферма

Вспомним малую теорему Ферма:

Малая теорема Ферма

Для любого простого $p$ и любого $1 \leqslant a \leqslant p-1$ выполняется $a^{p-1} \equiv 1(\bmod p)$.

На основе этой теоремы можно проверять $n$ на простоту следующим тестом: возьмём случайное $1 \leqslant a \leqslant n-1$ и проверим, правда ли, что $a^{n-1} \equiv 1(\bmod n)$. Если сравнение не выполняется (то есть $n$ не прошло тест), то $n$ точно составное.

Проблема в том, что из того, что сравнение выполняется, совсем не следует, что $n$ простое. Например, $341=31 \cdot 11$ - составное, но $2^{340}=1024^{34} \equiv 1(\bmod 341)$. Можно пытаться бороться с этой проблемой, запуская тест несколько (s) раз с различными $a$.

1
2
3
4
5
6
7
8


# возвращает False, если n составное;
# возвращает True, если все проверки пройдены успешно
FermatTest(n):
    for i = 0..(s - 1):
        a = random(1, n - 1) # случайное число от 1 до n - 1
        if modExp(a, n - 1, n) != 1:
            return False # n точно составное
    return True # надеемся, что n простое

Время работы теста Ферма на $b$-битном числе $n-O(s b \cdot M(b))$.

Как нам поможет несколько запусков теста? Заметим во-первых, что если $a$ окажется не взаимно просто с $n$ (то есть $\operatorname{gcd}(a, n) \neq 1)$, то $a^{n-1} \not \equiv 1(\bmod n)$, потому что такое $a$ не обратимо по модулю $n$. Это замечание, однако, не очень полезно, потому что таких $a$ может быть мало (например, если $n$ - произведение двух больших простых чисел), тогда вероятность случайно наткнуться на них невелика.

Зато можно доказать, что если $a^{n-1} \not \equiv 1(\bmod n)$ хотя бы для одного $a$, взаимно простого с $n$, то сравнение не выполняется и для многих других $a$ тоже:

Напомним, что $\mathbb{Z}_{n}$ - кольцо вычетов по модулю $n ; \mathbb{Z}_{n}^{*}$ - мультипликативная группа обратимых элементов кольца вычетов по модулю $n$.

Предложение

Пусть нашлось $a^{\prime}$ такое, что $\operatorname{gcd}\left(a^{\prime}, n\right)=1,\left(a^{\prime}\right)^{n-1} \not \equiv 1(\bmod n)$. Тогда

$$\left|\left\{a: 1 \leqslant a < n, a^{n-1} \not \equiv 1 \quad(\bmod n)\right\}\right| \geqslant \frac{n-1}{2}$$

Доказательство

Рассмотрим множество из всех остальных $a$ :

$$A=\left\{a: 1 \leqslant a < n, a^{n-1} \equiv 1 \quad(\bmod n)\right\}$$

Нужно показать, что $|A| \leqslant \frac{n-1}{2}$. Заметим, что $A$ - подгруппа $\mathbb{Z}_{n}^{*}$. При этом по условию леммы $a^{\prime} \in \mathbb{Z}_{n}^{*} \backslash A$, поэтому $A-$ собственная подгруппа. Поскольку порядок подгруппы делит порядок группы, $|A| \leqslant \frac{\left|\mathbb{Z}_{n}^{*}\right|}{2} \leqslant \frac{n-1}{2}$.

Таким образом, если существует хоть одно $a$, взаимно простое с $n$ и такое, что $a^{n-1} \not \equiv 1(\bmod n)$, то $n$ не пройдёт тест со случайным а с вероятностью хотя бы $\frac{1}{2}$. Значит, алгоритм, запустивший тест $s$ раз, ошибётся и назовёт такое составное число $n$ простым с вероятностью не больше, чем $\frac{1}{2^{s}}$. Скажем, при $s=50$ вероятность ошибки не превосходит $2^{-50}$, что уже пренебрежимо мало.

Числа Кармайкла

K сожалению, существуют составные числа $n$, для которых сравнение $a^{n-1} \equiv 1(\bmod n)$ выполняется для всех $a$, взаимно простых с $n$. Такие $n$ называются числами Кармайкла. Наименьшее число Кармайкла равняется $561=3 \cdot 11 \cdot 17$. Тест Ферма поймёт, что число Кармайкла $n$ составное, только если случайно наткнётся на $a$, имеющее с $n$ общий делитель, вероятность чего мала.

Чисел Кармайкла бесконечно много, но при этом они встречаются достаточно редко. Пусть $C(n)$ - количество чисел Кармайкла, не превосходящих $n$. Известно, что $C(n)>$ $n^{2 / 7}$ для достаточно больших $n$, но, с другой стороны, $\frac{C(n)}{n}$ стремится к нулю с ростом $n$. Поэтому большие простые числа иногда генерируют следующим образом: берут случайное число заданной длины, и проверяют его тестом Ферма (иногда даже не случайными $a$, а $a=2,3, \ldots$ ). Если длина числа большая, то вероятность того, что оно оказалось числом Кармайкла, невелика, тогда теста Ферма вполне достаточно.

Если же хочется проверить на простоту конкретное число, тестом Ферма не обойтись.

Тест Миллера-Рабина

Тест Миллера-Рабина (Artjuhov, 1967; Miller, 1976; Rabin, 1980) делает более тонкую проверку, которая работает и в случае чисел Кармайкла.

Определение

Назовём $a$ нетривиальным корнем из единицы по модулю $n$, если $a^{2} \equiv 1(\bmod n)$, но $a \not \equiv \pm 1(\bmod n)$.

Лемма

Нетривиальных корней по простому модулю $p$ не существует.

Доказательство

Доказательство. По модулю 2 есть всего два остатка - $0$ и $1 \equiv-1$, ясно, что $0$ - не корень из единицы. Дальше считаем $p \geqslant 3$.

Если $a^{2} \equiv 1(\bmod p)$, то $(a-1)(a+1)$ делится на $p . \operatorname{gcd}(a-1, a+1) \leqslant 2$, а $p \geqslant 3$, тогда либо $a-1$ делится на $p$, и $a \equiv 1(\bmod p)$, либо $a+1$ делится на $p$, и $a \equiv-1$ $(\bmod p)$.

Тест Миллера-Рабина помимо проверки условия из теоремы Ферма пытается найти нетривиальный корень из единицы по модулю $n$. Делается это следующим образом: пусть дано нечётное $n$ (чётные числа проверять на простоту очень просто). Из чётного числа $n-1$ выделяются все степени двойки: $n-1=2^{k} m$ для $k \geqslant 1$ и нечётного $m$. После этого вычисляется последовательность $a^{m} \bmod n, a^{2 m} \bmod n, \ldots, a^{2^{k} m} \bmod n=a^{n-1} \bmod n$.

Если $a^{n-1} \not \equiv 1(\bmod n)$, то, как и в тесте Ферма, мы делаем вывод, что число составное. Иначе найдём в последовательности первую единицу, и посмотрим на элемент перед ней. Если он есть (то есть последовательность состоит не только из единиц), и он не равен $-1 \bmod n$, то мы нашли нетривиальный корень из единицы по модулю $n$, то есть $n$ - составное.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


# возвращает False, если n составное;
# возвращает True, если все проверки пройдены успешно
MillerRabinTest(n):
    m}=\textrm{n}-1,\textrm{k}=0\mathrm{ # найдём k, m такие, что n - 1 = m * 2 ** k
    while m % 2 == 0:
        m /= 2, k += 1
    for i = 0..(s - 1):
        a = random(1, n - 1) # случайное число от 1 до n - 1
        x = modExp(a, m, n)
        for j = 0..(k - 1):
            y = x * x mod n
            if y == 1 and x != 1 and x != n - 1:
                return False # нашли нетривиальный корень из единицы, т.е. n - составное
            x = y
        if x != 1:
            return False # не выполнилось условие теоремы Ферма, т.е. n - составное
    return True # надеемся, что n простое

Время работы $s$ раундов теста Миллера-Рабина на $b$-битном числе - снова $O(s b \cdot M(b))$.

Оценка вероятности ошибки

Назовём $1 \leqslant a \leqslant n-1$ свидетелем непростоты $n$, если $n$ не проходит тест Миллера-Рабина при использовании $a$, то есть если $a^{n-1} \not \equiv 1(\bmod n)$; либо если для некоторого $0 \leqslant j

Теорема

Пусть $n$ - нечётное составное; $n-1=2^{k} m$, где $k \geqslant 1$, $m$ - нечётное. Тогда существует хотя бы $\frac{n-1}{2}$ свидетелей непростоты $n$.

Доказательство

Мы можем считать, что $n$ - число Кармайкла, так для остальных $n$ утверждение теоремы следует из предложения 10.3.2. Рассмотрим два случая - либо $n=p^{t}$ для некоторого простого $p$ и $t \geqslant 2$, либо $n=n_{1} n_{2}$ для некоторых взаимно простых $n_{1}>1$ и $n_{2}>1$.

Пусть $n=p^{t}$, тогда рассмотрим $a=1+p^{t-1}$. Заметим, что

$$a^{n}=\left(1+p^{t-1}\right)^{p^{t}}=1+p^{t-1} \cdot p^{t}+\left(p^{t-1}\right)^{2} \cdot(\cdots) \equiv 1 \quad\left(\bmod p^{t}\right)$$

Тогда $a^{n-1} \not \equiv 1(\bmod n)\left(\right.$ так как в этом случае было бы верно $\left.a^{n} \equiv a(\bmod n)\right)$, то есть мы нашли $a$, взаимно простое с $n$, но не проходящее даже тест Ферма. Это противоречит предположению, что $n$ - число Кармайкла.

Значит, $n=n_{1} n_{2}$ для некоторых взаимно простых нечётных $n_{1}, n_{2}$. Рассмотрим максимальное $0 \leqslant j

Если $B$ - множество чисел от 1 до $n-1$, не являющихся свидетелями непростоты, то

$$B \subset B^{\prime}=\left\{b \in \mathbb{Z}_{n}^{*}: b^{2^{j} m} \equiv \pm 1 \quad(\bmod n)\right\}$$

Заметим, что $B^{\prime}$ - подгруппа $\mathbb{Z}_{n}^{*}$, поэтому если мы покажем, что $\mathbb{Z}_{n}^{*} \backslash B^{\prime}$ непусто, то сразу получим

$$|B| \leqslant\left|B^{\prime}\right| \leqslant \frac{\left|\mathbb{Z}_{n}^{*}\right|}{2} \leqslant \frac{n-1}{2}$$

По китайской теореме об остатках, существует такое $w$, что

$$w \equiv v \quad\left(\bmod n_{1}\right), w \equiv 1 \quad\left(\bmod n_{2}\right)$$

Заметим, что

$$w^{2^{j} m} \equiv v^{2^{j} m} \equiv-1 \quad\left(\bmod n_{1}\right), w^{2^{j} m} \equiv 1 \quad\left(\bmod n_{2}\right)$$

значит, $w^{2^{j} m} \not \equiv \pm 1(\bmod n)$. С другой стороны,

$$w^{2^{j+1} m} \equiv 1 \quad\left(\bmod n_{1}\right), w^{2^{j+1} m} \equiv 1 \quad\left(\bmod n_{2}\right)$$

то есть $w^{2^{j+1} m} \equiv 1(\bmod n)$. Значит, $w \in \mathbb{Z}_{n}^{*} \backslash B^{\prime}$, что завершает доказательство теоремы.

Из теоремы следует, что для любого нечётного составного $n$ (в том числе для чисел Кармайкла), доля $a$, являющихся свидетелями непростоты, есть хотя бы $\frac{1}{n-1} \cdot \frac{n-1}{2}=\frac{1}{2}$, то есть вероятность ошибки после $s$ раундов теста не превосходит $2^{-s}$. На самом деле можно показать, что свидетелей непростоты ещё больше, и вероятность ошибки на каждом шаге не превосходит $\frac{1}{4}$.

✍️ В 2002 году был изобретён детерминированный тест простоты, работающий за полиномиальное от длины числа время. Время работы теста AKS (Agrawal, Kayal, Saxena, 2002) на $b$-битном числе в первой публикации оценивалось как $O\left(b^{12+\varepsilon}\right)$, впоследствии оценка была улучшена до $O\left(b^{6+\varepsilon}\right)(\varepsilon$ - сколь угодно малое положительное число, под $O\left(b^{\varepsilon}\right)$ имеется в виду какая-то степень $\left.\log b\right)$. Однако вероятностные тесты всё равно работают намного быстрее, поэтому на практике этот тест не используется.

✍️ Пусть $\pi(n)$ - количество простых чисел, не превосходящих $n$. Известно, что $\lim _{n \rightarrow \infty} \frac{\pi(n)}{n / \ln n}=1$. Значит, вероятность того, что случайное число из $b$ бит окажется простым, стремится к $\frac{1}{\ln 2^{b}} \approx \frac{1.44}{b}$ с ростом $b$. Тогда большие простые числа можно находить, просто много раз генерируя случайное число и проверяя его каким-нибудь тестом на простоту, пока тест не окажется пройден. Если генерировать $b$-битное число, в среднем понадобится порядка $b$ попыток.

$\rho$-алгоритм Полларда

Задачу факторизации числа не умеют решать за время, полиномиальное от длины битовой записи числа. Тем не менее, существуют алгоритмы, работающие эффективнее перебора всех потенциальных делителей до корня из числа. $\rho$-алгоритм Полларда (1975) с вероятностью, близкой к единице, находит нетривиальный делитель составного $b$-битного числа $n$ за $O\left(n^{\frac{1}{4}} b^{2}\right)=O\left(2^{\frac{b}{4}} b^{2}\right)$ шагов. Делается это следующим образом: выбирается специальная функция $f: \mathbb{Z}_{n} \rightarrow \mathbb{Z}_{n}$, действующая на остатках по модулю $n$ (обычно используют $f(x)=\left(x^{2}+1\right) \bmod n$ ), а также остаток $0 \leqslant x_{0}

Пусть $p$ - минимальный нетривиальный делитель $n$, обозначим $x_{i}^{\prime}=x_{i} \bmod p$. Рано или поздно какое-то значение $x_{i}^{\prime}$ встретится второй раз (то есть совпадёт с $x_{j}^{\prime}, j

Если $x_{i}^{\prime}=x_{j}^{\prime}$, то $x_{i}-x_{j}$ делится на $p$, тогда $\operatorname{gcd}\left(x_{j}-x_{i}, n\right)>1$. Более того, поскольку вычисление $f(x)$ состоит из применения нескольких сложений и умножений, из $x_{i} \bmod p=$ $x_{j} \bmod p$ следует, что $f\left(x_{i}\right) \bmod p=f\left(x_{j}\right) \bmod p$, то есть $x_{i+1}^{\prime}=x_{j+1}^{\prime}$. Тогда по индукции $\operatorname{gcd}\left(x_{j+k}-x_{i+k}, n\right)>1$ для любого $k \geqslant 0$.

Тогда можно поступить следующим образом: будем вычислять одновременно две последовательности: $x_{i}=f\left(x_{i-1}\right)$ и $y_{0}=x_{0}, y_{i}=f\left(f\left(y_{i-1}\right)\right)$, и на каждом шаге вычислять $\operatorname{gcd}\left(y_{i}-x_{i}, n\right)$, пока он не окажется больше единицы.

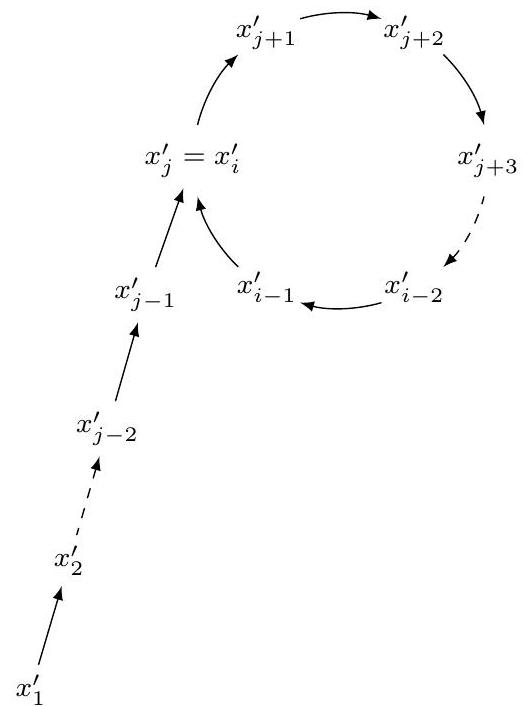
За первые $O(\sqrt{p})$ шагов значения $x_{i}$ по модулю $p$ с большой вероятностью начнут повторяться (то есть $x_{i}$ попадёт на цикл на рисунке¹). В этот момент $y_{i}$ тоже уже будет находиться на этом цикле, причём на каждой следующей итерации $y_{i}$ будет делать два шага вперёд по циклу, а $x_{i}$ только один. Тогда ещё за $O(\sqrt{p})$ шагов $y_{i}$ “догонит” $x_{i}$, то есть для какого-то $i$ окажется верным $x_{i} \bmod p=y_{i} \bmod p$, откуда $\operatorname{gcd}\left(y_{i}-x_{i}, n\right)>1$, значит мы найдём делитель $n$, больший единицы.

Заметим, что совсем не обязательно $\operatorname{gcd}\left(y_{i}-x_{i}, n\right)$ окажется равным $p$. $y_{i}$ и $x_{i}$ могут в тот же момент времени оказаться на одной позиции в цикле и по какому-нибудь другому модулю $q$, где $q$ - делитель $n$. Может даже оказаться, что $\operatorname{gcd}\left(y_{i}-x_{i}, n\right)=n$, тогда алгоритм не даст нам никакой полезной информации. Но можно показать, что для достаточно больших $n$ вероятность этого мала (мы должны одновременно попасть на одну позицию в цикле по всем нетривиальным делителям $n$ ). В случае, если это случается, можно перезапустить алгоритм с другим $x_{0}$.

Как уже говорилось, в качестве $f$ обычно используют $f(x)=\left(x^{2}+1\right) \bmod n$ или $f(x)=\left(x^{2}-1\right) \bmod n$. Эти функции, конечно, не являются случайными, поэтому описанный выше анализ не является строгим доказательством времени работы алгоритма, а лишь эвристическими рассуждениями. Тем не менее, время работы алгоритма на практике хорошо согласуется с этими рассуждениями.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


rhoAlgorithm(n):
    y = x = random(0, n - 1) # случайное число от 0 до n - 1
    d = 1
    while d == 1:
        x}=(\textrm{x}*\textrm{x}+1)\operatorname{mod}\textrm{n
        y =(y*y + 1) mod n
        y = (y*y + 1) mod n
        d = gcd(x - y, n)
    if d == n:
        return rhoAlgorithm(n) # запустим алгоритм заново
    return d

Обычно число $n$ проверяют на простоту, прежде чем запускать на нём алгоритм Полларда. Если нужно целиком факторизовать $n$, то, получив нетривиальный делитель $d$,нужно проверить $d$ и $\frac{n}{d}$ на простоту, и, если надо, запустить алгоритм на них.

Алгоритм с большой вероятностью сделает не более $O(\sqrt{p})=O\left(n^{\frac{1}{4}}\right)$ шагов (так как минимальный делитель $p$ не больше корня из $n$ ), на каждом шаге происходит вычисление gcd , поэтому время работы на $b$-битном числе $n$ можно оценить как $O\left(n^{\frac{1}{4}} b^{2}\right)$.

Оценка времени работы

Покажем, что если бы $f$ действительно была случайной функцией, то значения $x_{i}^{\prime}=$ $x_{i} \bmod n$ с большой вероятностью начали бы повторяться за первые $O(\sqrt{p})$ шагов. Поскольку мы будем работать с последовательностью $x_{i}^{\prime}$, для удобства будем считать, что $x_{0}$ - случайный остаток по модулю $p, f$ определена на остатках по модулю $p$.

Теорема

Пусть $p$ - минимальный нетривиальный делитель составного $n$. Пусть $f: \mathbb{Z}_{p} \rightarrow \mathbb{Z}_{p}$ и $x_{0} \in \mathbb{Z}_{p}$ выбраны случайно, $\lambda>0$. Рассмотрим последовательность, определённую правилом $x_{i}=f\left(x_{i-1}\right), 0 < i \leqslant l=1+\lfloor\sqrt{2 \lambda p}\rfloor$. Вероятность того, что все $x_{i}$ попарно различны, не превосходит $e^{-\lambda}$.

Доказательство

Всего различных пар $\left(f, x_{0}\right)-p^{p} \cdot p=p^{p+1}$. Всего пар $\left(f, x_{0}\right)$, для которых все элементы последовательности окажутся попарно различны - $p \cdot(p-1) \cdots(p-l) \cdot p^{p-l}$, так как $x_{0}$ мы выбираем произвольно; $f\left(x_{0}\right) \neq x_{0} ; f\left(x_{1}\right) \neq x_{0}, x_{1} ; \ldots ; f\left(x_{l}\right) \neq x_{0}, x_{1}, \ldots, x_{l}$; остальные значения $f$ произвольные.

Тогда доля пар $\left(f, x_{0}\right)$, соответствующих последовательностям без повторений, равна

$$\prod_{i=1}^{l}\left(1-\frac{i}{p}\right)$$

Чтобы показать, что эта доля не превосходит $e^{-\lambda}$, достаточно показать, что

$$\sum_{i=1}^{l} \ln \left(1-\frac{i}{p}\right) \leqslant-\lambda$$

Докажем это неравенство:

$$\sum_{i=1}^{l} \ln \left(1-\frac{i}{p}\right)<-\sum_{i=1}^{l} \frac{i}{p}=-\frac{l(l+1)}{2 p}<-\frac{l^{2}}{2 p}<-\frac{2 \lambda p}{2 p}=-\lambda$$

Первое неравенство следует из того, что функция $f(x)=\ln (1-x)+x$ отрицательна при $0 < x < 1$, так как $f(0)=0, f^{\prime}(x)=-\frac{1}{1-x}+1=-\frac{x}{1-x} < 0$ при $0 < x < 1$. Последнее неравенство следует из того, что $l>\sqrt{2 \lambda p}$.

✍️ Существуют и более быстрые алгоритмы факторизации. Например, время работы алгоритма GNFS (general number field sieve) эвристически оценивается как $O\left(e^{(64 / 9)^{1 / 3}(\log n)^{1 / 3}(\log \log n)^{2 / 3}}\right)$.

траектория последовательности $x_{i}^{\prime}$ напоминает букву $\rho$, отсюда и пошло название алгоритма ↩︎