1. Анализ сложности алгоритмов

1. Вычисление чисел Фибоначчи

Последовательность чисел Фибоначчи

определяется следующим образом:

Числа Фибоначчи растут экспоненциально быстро:

Экспоненциальный алгоритм

Следующий рекурсивный алгоритм вычисляет $n$-ое число Фибоначчи, точно следуя определению:

fib(n):
    if n <= 1:
        return 1
    return fib(n - 1) + fib(n - 2)

Каково время работы этого алгоритма? Оценим $T(n)$ - суммарное количество вызовов fib , происходящих при выполнении $\mathrm{fib}(\mathrm{n})$ : если $n \leqslant 1$, то $T(n)=1$; иначе

Несложно доказать по индукции, что $F_{n} \leqslant T(n)<2 F_{n}$. В каждом вызове fib совершается ограниченное число (скажем, не больше пяти) операций, поэтому время работы алгоритма примерно пропорционально $F_{n}$ (чуть позже у нас появится формальное определение этого “примерно”).

Из леммы 1.1.1 следует, например, что, $F_{300} \geqslant 2^{150}>10^{45}$. На компьютере, выполняющем $10^{9}$ операций в секунду, fib(300) будет выполняться больше $10^{36}$ секунд.

Полиномиальный алгоритм

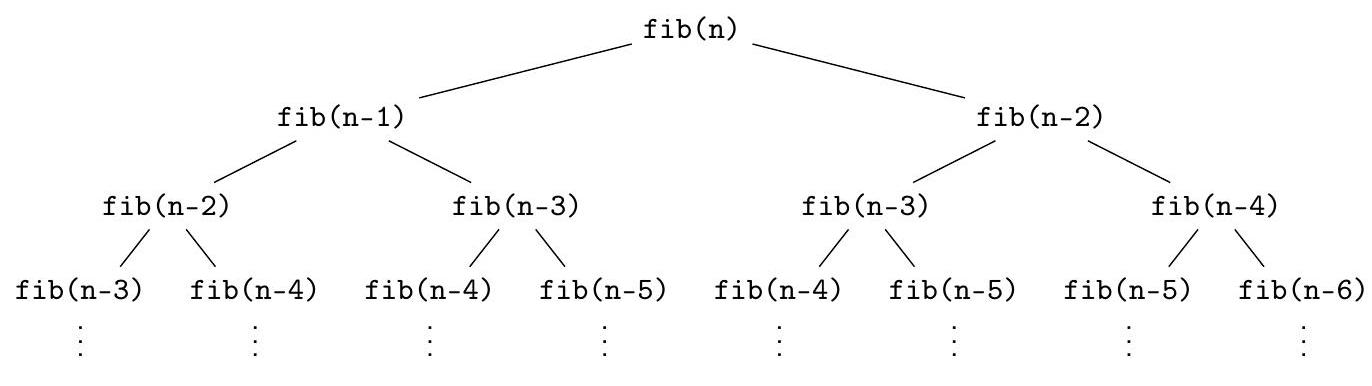
Посмотрим на дерево рекурсивных вызовов алгоритма fib (рис. 1.1). Видно, что алгоритм много раз вычисляет одно и то же. Давайте сохранять результаты промежуточных вычислений в массив:

Рис. 1.1: Дерево рекурсивных вызовов fib

fibFast(n):
    if n <= 1:
        return 1
    int f[n + 1] # создаём массив с индексами 0..n
    f[0] = f[1] = 1
    for i = 2..n:
        f[i] = f[i - 1] + f[i - 2]
    return f[n]

На каждой итерации цикла совершается одно сложение, всего итераций примерно $n$, поэтому количество сложений, выполняемых в ходе нового алгоритма, примерно пропорционально $n$. Есть ещё одна тонкость - из леммы 1.1.1 следует, что двоичная запись $F_{n}$ имеет длину порядка $n$. Чуть позже мы увидим, что сложение двух $n$-битовых чисел требует порядка $n$ элементарных операций, значит общее время работы нового алгоритма примерно пропорционально $n^{2}$. С помощью fibFast можно уже за разумное время вычислить не только $F_{300}$, но и $F_{100000}$.

1.2 О-символика

Хорошо себя зарекомендовал и стал общепринятым следующий подход - оценивать время работы алгоритма некоторой функцией от входных параметров, при этом пренебрегая ограниченными множителями. Это позволяет эффективно сравнивать алгоритмы между собой, при этом не нужно заниматься точным подсчётом количества элементарных операций. Примерно так мы и рассуждали об алгоритмах вычисления чисел Фибоначчи. Введём несколько обозначений, которые помогут проводить подобные рассуждения более кратко и точно.

Время работы алгоритма - это, конечно, всегда неотрицательная функция. Тем не менее, мы даём следующие определения для функций, принимающих произвольные вещественные значения, поскольку такие функции часто возникают в процессе рассуждений.

Запись $f=O(g)$ можно понимать как " $|f| \leqslant|g|$ с точностью до константы". Аналогично, $\Omega(\cdot)$ можно считать аналогом $\geqslant$, а $\Theta(\cdot)$ - аналогом $=$. Ещё один способ понимать запись $f=O(g)$ - отношение $\frac{|f(n)|}{|g(n)|}$ ограничено сверху некоторой константой.

Многие естественные свойства операторов сравнения $\leqslant,=, \geqslant$ выполняются и для их асимптотических аналогов. Сформулируем некоторые из этих свойств:

Существуют также асимптотические аналоги $<$ и $>: o(\cdot)$ и $\omega(\cdot)$.

Запись $f=o(g)$ можно понимать как “отношение $\frac{|f(n)|}{|g(n)|}$ стремится к нулю с увеличением $n$ “, а запись $f=\omega(g)$ - как “отношение $\frac{|f(n)|}{|g(n)|}$ стремится к бесконечности с увеличением $n$ “.

Заметим, что у последних трёх свойств нет аналогов для обычных операторов сравнения.

Вернемся к алгоритмам вычисления чисел Фибоначчи. Пользуясь новыми обозначениями, мы показали, что время работы fibFast(n) можно оценить как $O\left(n^{2}\right)$. При этом время работы $\mathrm{fib}(\mathrm{n})$ можно оценить (сверху) как $O\left(2^{n} \cdot n\right)$, и (снизу) как $\Omega\left(2^{\lfloor n / 2\rfloor}\right)$.

1.3 Многочлены, экспоненты и логарифмы

Очень часто время работы алгоритма удаётся оценить функцией, являющейся комбинацией каких-то из трёх базовых типов: многочленов, экспонент и логарифмов. Так, время работы fibFast мы оценили многочленом $n^{2}$, а время работы fib - произведением экспоненты на многочлен: $2^{n} \cdot n$. В связи с этим полезно изучить асимптотические свойства этих функций и научиться сравнивать их между собой.

Под $\log n$ без указания основания мы будем иметь в виду $\log _{2} n$.

Если $n \in \mathbb{N}$, то $1+\left\lfloor\log _{b} n\right\rfloor$ - это количество цифр в $b$-ичной записи $n$.

Видим, что $\log _{a} n$ отличается от $\log _{b} n$ в константу $\left(\frac{1}{\log _{b} a}\right)$ раз, то есть $\log _{a} n=\Theta\left(\log _{b} n\right)$ для любых оснований $a, b$. Поэтому для удобства часто используют записи вида $O(\log n)$, не уточняя основание.