13. Графы. Поиск в глубину

Большая часть рассуждений применима как к ориентированным, так и к неориентированным графам (если не сказано обратное); допускаются кратные рёбра и петли (если не сказано обратное).

Обход вершин, достижимых из данной

Поиск в глубину (depth-first search, DFS) по вершине $w \in V$ находит множество вершин, достижимых из неё, то есть таких, в которые можно попасть, сделав несколько переходов по рёбрам, начиная из вершины $w$.

Изначально алгоритм запускается от вершины $w$. Он перебирает исходящие из текущей вершины рёбра и смотрит, куда они ведут. Каждый раз, когда алгоритм встречает ещё не посещённую вершину, он запускается от неё рекурсивно, а после возврата из рекурсии продолжает перебирать рёбра, исходящие из текущей вершины.

1
2
3
4
5
6
7
8

dfs(v):
    visited[v] = True
    for u in es[v]: # es[v] - список смежности вершины v
        if not visited[u]:
            dfs(u)
fill(visited, False)
dfs(w)
# visited[u] = True, если u достижима из w

Почему алгоритм посетил все достижимые из $w$ вершины? Пусть $u$ достижима из $w$, тогда существует путь (path) из $w$ в $u$ - последовательность вершин $w=v_{1}, v_{2}, \ldots, v_{k}=u$, в которой для $1 \leqslant i < k$ есть ребро из $v_{i}$ в $v_{i+1}$ (путём, в зависимости от контекста, мы будем называть как такую последовательность вершин, так и последовательность соединяющих их рёбер). Пусть $v_{i}$ - первая вершина на пути, которую не посетил алгоритм. Тогда он посетил $v_{i-1}$ и проверил ребро, ведущее из $v_{i-1}$ в $v_{i}$, что противоречит тому, что он не посетил $v_{i}$.

Время работы алгоритма (при использовании списков смежности) $-O(V+E)$, так как каждая вершина посещена не более одного раза, время обработки каждой посещённой вершины пропорционально её исходящей степени, сумма исходящих степеней не превосходит числа рёбер в графе (удвоенного числа рёбер в неориентированном графе).

Компоненты связности

Неориентированный граф называется связным (connected), если в нём существует путь между любой парой вершин.

На произвольном графе можно ввести отношение достижимости: $a \sim b$, если $b$ достижимо из $a$. Это отношение рефлексивно ( $a \sim a$ ) и транзитивно (если $a \sim b$ и $b \sim c$, то $a \sim c$ ). В неориентированных графах это отношение ещё и симметрично (если $a \sim b$, то $b \sim a$ ), поэтому оно является отношением эквивалентности: все вершины однозначно разбиваются на классы эквивалентности - множества, в каждом из которых любые две вершины достижимы друг из друга; при этом любые две вершины из разных классов эквивалентности не достижимы друг из друга (класс эквивалентности вершины - это просто множество вершин, достижимых из неё; из рефлексивности, транзитивности и симметричности следует, что для разных вершин такие множества либо не пересекаются, либо совпадают).

Индуцированные подграфы на каждом из этих классов эквивалентности называют компонентами связности (connected components) (иногда компонентами связности будем называть сами классы эквивалентности, то есть множества вершин этих подграфов). Каждая компонента связности является связным подграфом, при этом рёбер между вершинами из разных компонент связности в графе нет. Связный граф состоит из одной компоненты связности, содержащей все вершины.

В ориентированных графах отношение ~ не симметрично, поэтому понятие “компонента связности” для них не определено. Есть понятие сильной связности, которое мы обсудим чуть позже.

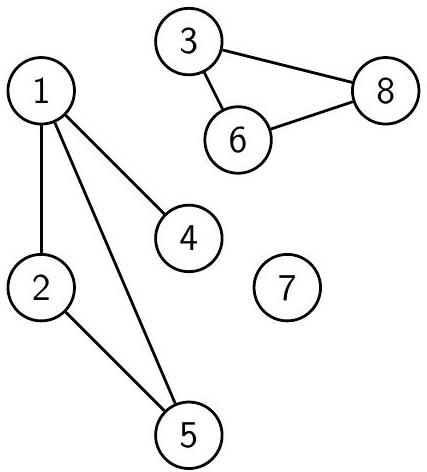
Компоненты связности этого графа - $\{1,2,4,5\}$, $\{3,6,8\}$ и $\{7\}$

Алгоритм поиска в глубину по вершине находит все достижимые из неё вершины, то есть её компоненту связности. Тогда для того, чтобы найти все компоненты связности, запустим поиск в глубину из каждой вершины по очереди. Для того, чтобы не обрабатывать одну компоненту связности несколько раз, просто не будем обнулять пометки того, была ли вершина посещена, между запусками алгоритма от разных вершин. Если очередная рассматриваемая вершина уже посещена, то она входит в одну из уже найденных компонент связности. Значит, запускать алгоритм от неё не надо.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

vector<vector<int> > components
dfs(v):
    visited[v] = True
    components.back().push_back(v)
    for u in es[v]:
        if not visited[u]:
            dfs(u)
fill(visited, False)
for v = 0..(n - 1): # вершины пронумерованы от 0 до n - 1
    if not visited[v]:
        components.push_back(vector<int>())
        dfs(v)

Время работы алгоритма - по-прежнему $O(V+E)$, так как каждую вершину алгоритм теперь посещает ровно один раз.

Дерево(лес) поиска в глубину неориентированного графа

Пусть $G=(V, E)$ - связный граф, из вершины $v \in V$ которого был запущен поиск в глубину. Рассмотрим остовный подграф $H=(V, F)$, где $F$ - множество рёбер, при рассмотрении которых алгоритм делал рекурсивный запуск (рёбер, которые вели в ещё не посещённые вершины). Заметим, что $H$ - связный граф, так как поиск в глубину на связном графе $G$ посетил все вершины.

Цикл - это путь с совпадающими концами и ненулевым числом рёбер, все рёбра в котором различны. Граф $H$ не содержит циклов: ориентируем рёбра $H$ в сторону вершины, которая была непосещённой в момент прохода по ребру алгоритмом; в каждую вершину входит не более одного ребра $H$. Но если бы нашёлся цикл, то в ту вершину цикла, которая была посещена алгоритмом позже всех, вело бы сразу два ребра.

Итак, $H$ - связный граф без циклов, то есть дерево. Если ориентировать рёбра этого дерева, как сказано выше, получится корневое дерево (корень - вершина $v$ ). Мы снова будем пользоваться терминами, которыми пользовались при изучении двоичных куч: ребёнок, родитель, потомок, предок, лист и так далее.

$H$ называют деревом поиска в глубину графа $G$. Конечно, дерево поиска в глубину не единственно: оно зависит от начальной вершины и порядка рёбер в списках смежности.

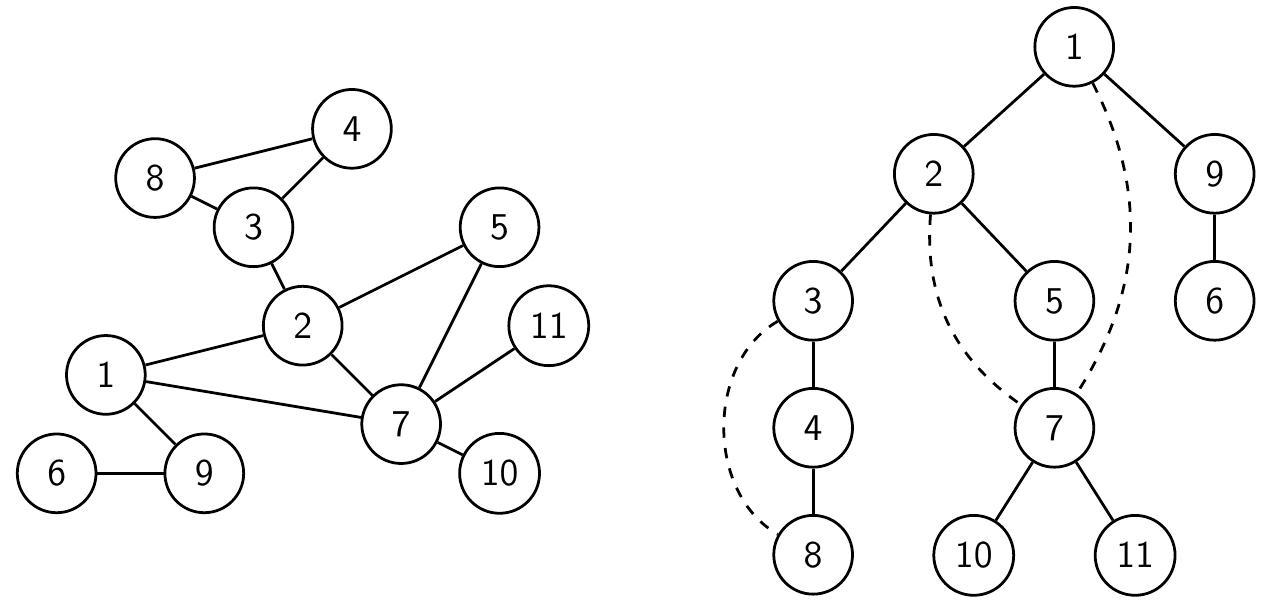
Связный граф и дерево поиска в глубину (поиск запущен из вершины 1, в списках смежности вершины упорядочены по возрастанию номеров)

Ребро графа $G$, не являющееся ребром дерева поиска в глубину (то есть любое ребро из $E \backslash F$ ) будем называть обратным (back edge). Рассмотрим любое обратное ребро $e=(v, u)$. Пусть вершину $v$ алгоритм посетил раньше вершины $u$. Тогда вершина $u$ была посещена после вершины $v$, но до того, как алгоритм рассмотрел ребро $e$, то есть $u$ была посещена в одном из рекурсивных вызовов, произошедших во время обработки $v$. Значит, в дереве поиска в глубину $u$ является потомком $v$.

Итак, любое обратное ребро соединяет пару “предок-потомок”. Значит, в графе нет перекрёстных рёбер - рёбер, соединяющих пары вершин, ни одна из которых не является потомком другой в дереве поиска в глубину.

Лес поиска в глубину

При поиске компонент связности в несвязном графе получается своё дерево поиска в глубину в каждой компоненте связности. Их совокупность - лес поиска в глубину. Все рёбра графа снова делятся на рёбра деревьев и обратные рёбра; рёбер между разными деревьями нет.

Поиск цикла в неориентированном графе

Как проверить, есть ли в неориентированном графе цикл? Поскольку деревья поиска в глубину не имеют циклов, любой цикл будет проходить хотя бы через одно обратное ребро. С другой стороны, любое обратное ребро $e=(v, u)$ соответствует циклу в графе: если $v$ - предок $u$, то поднимемся по дереву из $u$ в $v$, и вернёмся в $u$ по ребру $e$. Значит, в графе есть цикл тогда и только тогда, когда при поиске в глубину нашлось хотя бы одно обратное ребро.

Как отличить обратное ребро от ребра дерева? Если граф простой, то обратное ребро любое ребро, которое ведёт в уже посещённую вершину, не являющуюся родителем текущей в дереве поиска в глубину. То есть достаточно для каждой вершины запомнить её родителя (или просто передавать его отдельным параметром при рекурсивном запуске).

Если в графе имеются кратные рёбра, то надо хранить (передавать в рекурсивный запуск) не просто родителя вершины, а ещё и указатель на ребро дерева (или просто его номер, если рёбра пронумерованы), по которому мы пришли в текущую вершину из родителя. Так мы сможем отличить ребро дерева от других рёбер между той же парой вершин.

Если цикл нужно явно найти и вывести, то, обнаружив обратное ребро $e=(u, v)$, будем переходить, начиная из текущей вершины $u$, по ссылкам на родителя, пока не встретим $v$, и выписывать вершины на пути.

Времена входа и выхода

В процессе работы поиска в глубину для каждой вершины $v$ запомним время входа (время начала обработки вершины) $t_{i n}[v]$ и время выхода (время конца обработки вершины) $t_{\text {out }}[v]$. Для этого заведём специальный счётчик, который будем увеличивать на единицу каждый раз, когда происходит одно из этих событий; текущее значение этого счётчика и будет текущим временем.

1
2
3
4
5
6
7
8

T = 0 # счётчик времени
dfs(v):
    tin[v] = T, T += 1
    visited[v] = True
    for u in es[v]:
        if not visited[u]:
            dfs(u)
    tout[v] = T, T += 1

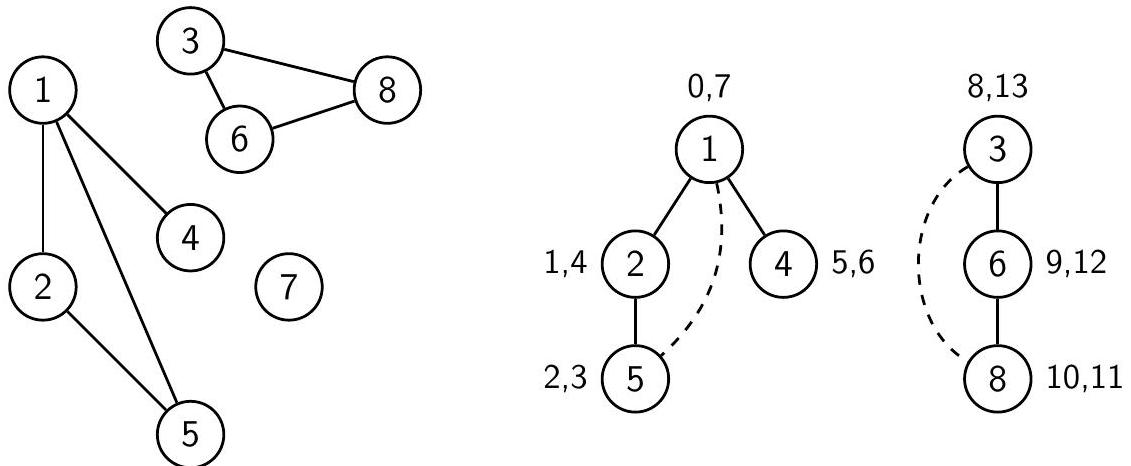
Граф и его лес поиска в глубину с отмеченными временами входа и выхода

Заметим, что если вершина $u$ начала обрабатываться в одном из рекурсивных вызовов, произошедших во время обработки другой вершины $v$, то $u$ закончит обрабатываться раньше, чем $v$. Значит, для любых вершин $v, u \in V$ либо отрезки $\left[t_{\text {in }}(v), t_{\text {out }}(v)\right]$ и $\left[t_{i n}(u), t_{\text {out }}(u)\right]$ не пересекаются, либо один из них содержится в другом. Более того, отрезок $u$ содержится в отрезке $v$ тогда и только тогда, когда $u$ является потомком $v$ в дереве поиска в глубину.

Времена входа и выхода имеют множество различных применений. Простой пример: пусть $G$ - корневое дерево; запустим поиск в глубину из корня $G$ и вычислим времена входа и выхода каждой вершины. Получившееся дерево поиска в глубину совпадает с графом $G$. Тогда мы можем за $O(1)$ проверить для любой пары вершин, является ли одна из них предком другой в $G$ : достаточно проверить, вложен ли отрезок времени обработки одной из вершин в отрезок другой вершины.

Дерево(лес) поиска в глубину ориентированного графа, типы рёбер

Дерево(лес) поиска в глубину определяются для ориентированных графов так же, как и для неориентированных: будем перебирать все вершины и запускать поиск в глубину из ещё не посещённых, не обнуляя пометки о посещённости в процессе.

Времена входа и выхода для ориентированных графов вычисляются так же, как и для неориентированных, при этом по прежнему либо отрезки времён обработки вершин не пересекаются, либо один из них вложен в другой.

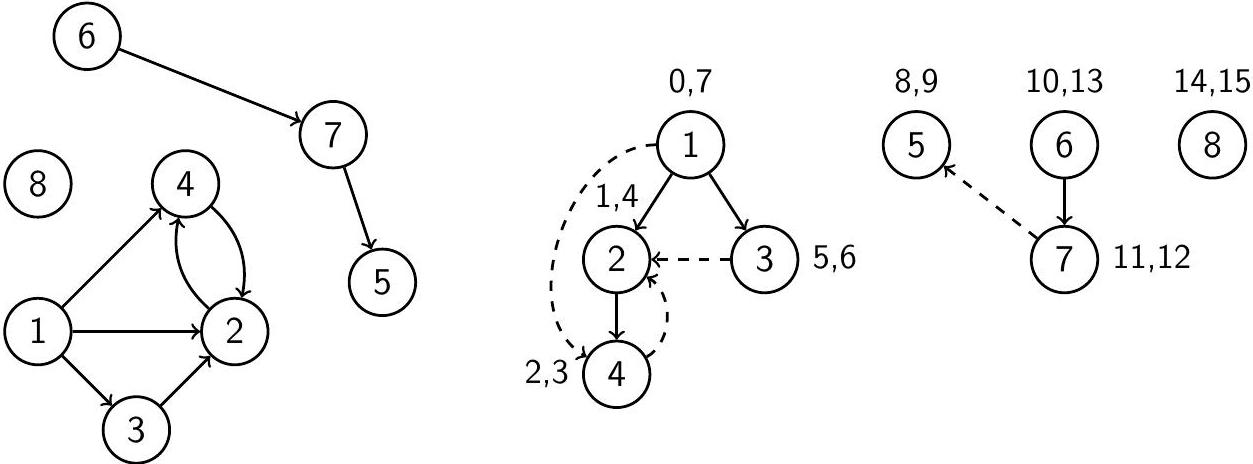
Граф и его лес поиска в глубину с отмеченными временами входа и выхода

В ориентированных графах рёбра, не вошедшие в лес поиска в глубину, делятся уже на три типа:

• прямые (forward) - ведущие от вершины к её потомку (ребро $1 \rightarrow 4$);
• обратные (back) - ведущие от вершины к её предку (ребро $4 \rightarrow 2$);
• перекрёстные (cross) - ведущие от вершины к другой вершине, не являющейся ни предком, ни потомком первой (рёбра $3 \rightarrow 2$ и $7 \rightarrow 5$). Понять тип ребра можно по временам входа и выхода его концов: ребро $v \rightarrow u$ является
• прямым (либо ребром леса), если $t_{\text {in }}(v) < t_{\text {in }}(u), t_{\text {out }}(u) < t_{\text {out }}(v)$;
• обратным, если $t_{\text {in }}(u) < t_{i n}(v), t_{\text {out }}(v) < t_{\text {out }}(u)$;
• перекрёстным, если $t_{\text {out }}(u) < t_{\text {in }}(v)$.

Заметим, что ситуация $t_{\text {out }}(v) < t_{\text {in }}(u)$ невозможна: в момент рассмотрения такого ребра вершина $u$ была бы непосещённой, тогда ребро вошло бы в дерево поиска в глубину, и было бы верно $t_{\text {in }}(u) < t_{\text {out }}(u) < t_{\text {out }}(v)$.

Поиск цикла в ориентированном графе

Как и в случае неориентированного графа, в ориентированном графе есть цикл тогда и только тогда, когда при поиске в глубину нашлось хотя бы одно обратное ребро: по

любому обратному ребру цикл строится точно так же, как и в неориентированном случае; с другой стороны, пусть в графе есть цикл $v_{1} \rightarrow v_{2} \rightarrow \cdots \rightarrow v_{k} \rightarrow v_{1}$, и вершину $v_{i}$ алгоритм обработал первой среди вершин цикла. Остальные вершины цикла достижимы из $v_{i}$, поэтому все они будут потомками $v_{i}$ в дереве поиска в глубину. Но тогда ребро $v_{i-1} \rightarrow v_{i}\left(v_{k} \rightarrow v_{1}\right.$ при $\left.i=1\right)$ является обратным.

Обратное ребро можно обнаружить при помощи времён входа и выхода. Альтернативный способ - для каждой вершины поддерживать пометку одного из трёх типов: “непосещённая”, “в обработке”, “обработана”. Тогда обратные рёбра - ровно те, что ведут в вершину с пометкой “в обработке”.

Топологическая сортировка

Ориентированный ациклический граф (directed acyclic graph, dag) - это ориентированный граф без циклов. С помощью ориентированных ациклических графов удобно представлять отношения зависимости: иерархические отношения (“руководитель-подчинённый”), причинно-следственные связи.

Топологическая сортировка (topological sort) ориентированного графа - это такой порядок на вершинах, что любое ребро графа ведёт из меньшей вершины в большую. Ясно, что граф, в котором есть цикл, топологически отсортировать невозможно.

Возникает вопрос: какие ациклические графы можно топологически отсортировать? Оказывается, что все: достаточно расположить вершины в порядке убывания времён выхода. Действительно, если нашлось такое ребро $v \rightarrow u$, что $t_{\text {out }}(v) < t_{\text {out }}(u)$, то это ребро обратное, значит, граф не ациклический.

Можно не вычислять времена входа и выхода напрямую, а просто добавлять вершину в конец списка в конце её обработки. Тогда вершины в списке окажутся в порядке возрастания времён выхода. Остаётся развернуть список в конце, чтобы получить порядок топологической сортировки.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

vector<int> topOrder # сюда запишем вершины в порядке топологической сортировки
dfs(v):
    visited[v] = True
    for u in es[v]:
        if not visited[u]:
            dfs(u)
    topOrder.push_back(v)
fill(visited, False)
for v = 0..(n - 1): # вершины пронумерованы от 0 до n - 1
    if not visited[v]:
        dfs(v)
reverse(topOrder.begin(), topOrder.end())

Исток (source) - это вершина ориентированного графа, в которую не входит рёбер. Сток (sink) - вершина, из которой, наоборот, не выходит рёбер. Заметим, что первая вершина в порядке топологической сортировки всегда является истоком, а последняя стоком. В частности, в любом ациклическом ориентированном графе всегда есть хотя бы по одному истоку и стоку (это утверждение несложно доказать и без использования топологической сортировки).

Компоненты сильной связности

Рассмотрим на произвольном ориентированном графе следующее отношение: $a \sim b$ ( $a$ сильно связно (strongly connected) с $b$ ), если одновременно $a$ достижимо из $b$, и $b$

достижимо из $a$. Такое отношение рефлексивно, транзитивно и симметрично, поэтому оно однозначно разбивает вершины графа на классы эквивалентности, которые называют компонентами сильной связности (strongly connected components). Граф, состоящий из одной такой компоненты, называют сильно связным (strongly connected graph).

Пусть $V_{1}, \ldots, V_{k}$ - компоненты сильной связности графа $G$. Построим вспомогательный граф, вершины которого $-V_{1}, \ldots, V_{k}$, а ребро $V_{i} \rightarrow V_{j}$ проведено, только если в $G$ было ребро $v_{i} \rightarrow v_{j}$ для некоторых $v_{i} \in V_{i}, v_{j} \in V_{j}$ (при этом не будем проводить петли и кратные рёбра). Получившийся граф называют метаграфом (meta-graph) или конденсацией графа $G$. Метаграф не содержит циклов, так как все вершины компонент сильной связности, вошедших в цикл, были бы одновременно достижимы друг из друга, то есть должны были бы лежать в одной компоненте.

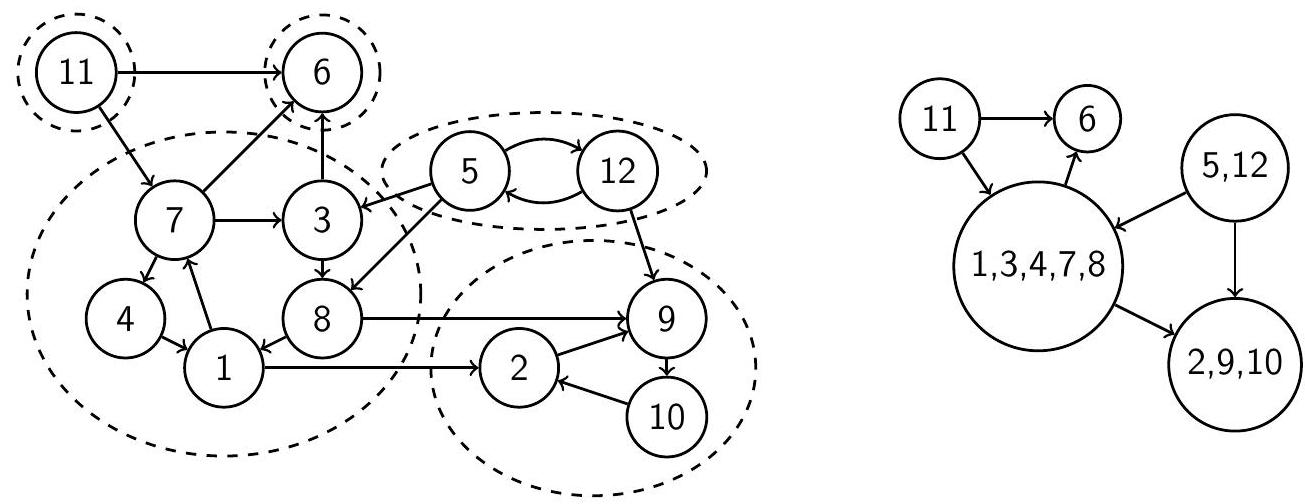
Ориентированный граф и его метаграф

Наша цель - научиться находить компоненты сильной связности произвольного ориентированного графа $G$ за $O(V+E)$. Первое, что мы сделаем - запустим алгоритм топологической сортировки на графе $G$. Он вернёт список вершин в порядке убывания времён выхода; обозначим этот список за $v_{1}, \ldots, v_{n}$. Этот список в общем случае не является порядком топологической сортировки (так как в $G$ могут быть циклы), но всё равно обладает полезными свойствами.

Отсюда следует, что метаграф можно топологически упорядочить, если расположить компоненты сильной связности в порядке убывания максимального значения времён выхода их вершин. В частности, $v_{1}$ принадлежит первой в топологическом порядке компоненте, то есть компоненте-истоку. Обозначим эту компоненту за $A_{1}$.

Как по одной вершине из компоненты-истока найти все вершины, лежащие в этой компоненте? Рассмотрим транспонированный граф (transpose graph) $G^{T}$, полученный из $G$ изменением направления всех рёбер. Заметим, что компоненты сильной связности $G^{T}$ совпадают (как множества вершин) с компонентами $G$, а метаграф $G^{T}$ является транспонированным графом метаграфа $G$. В частности, компонента-исток в метаграфе $G$ является компонентой-стоком в метаграфе $G^{T}$.

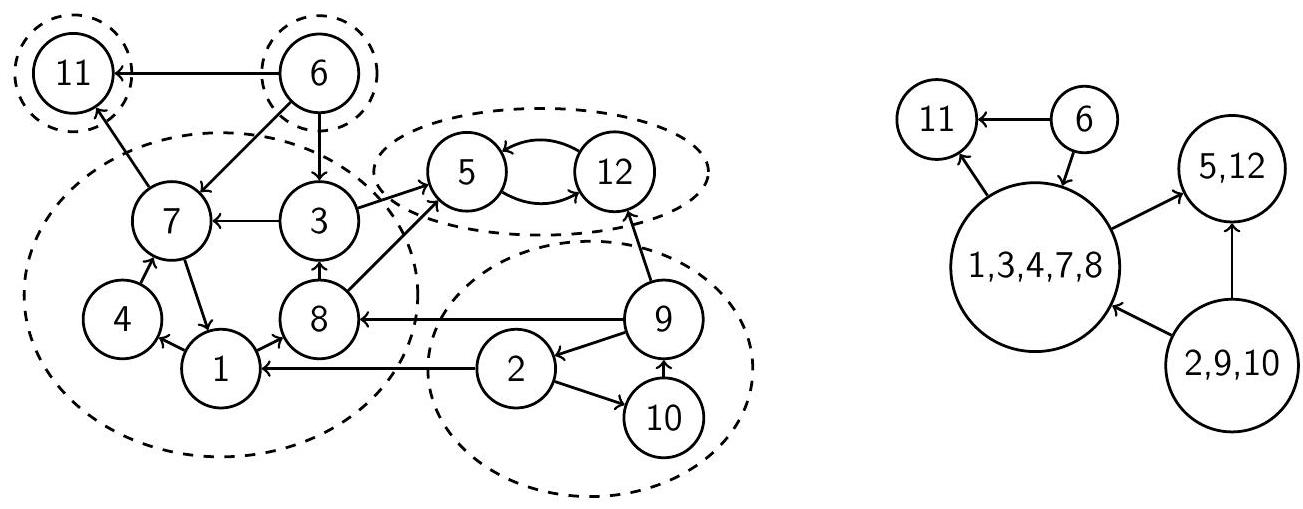
Транспонированный граф и его метаграф

Множество вершин, достижимых из любой вершины компоненты-стока, совпадает с этой компонентой. Значит, для того, чтобы найти $A_{1}$, можно запустить поиск в глубину в графе $G^{T}$ из $v_{1}$.

Как найти все остальные компоненты? Удалим из графа $G$ компоненту $A_{1}$ (обозначим полученный граф за $G_{1}$ ) и повторим те же действия: найдём $v_{i}$ - вершину с максимальным временем выхода из ещё не удалённых; $v_{i}$ лежит в компоненте-истоке $A_{2}$ графа $G_{1}$, которую можно найти, запустив поиск в глубину из $v_{i}$ в графе $G_{1}^{T}$. После этого удалим компоненту $A_{2}$ и тем же способом найдём следующую компоненту, и так далее, пока вершины не закончатся.

Удалять вершины и перестраивать списки смежности не нужно, можно просто считать посещённые вершины удалёнными.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

# уже найден topOrder - список вершин в порядке убывания времени выхода
vector<vector<int> > components
dfsT(v):
    visited[v] = True
    components.back().push_back(v)
    for u in esT[v]: # список смежности транспонированного графа
        if not visited[u]:
            dfsT(u)
fill(visited, False)
for v in topOrder: # перебираем вершины в порядке убывания времени выхода
    if not visited[v]:
        # v - вершина с максимальным временем выхода из ещё не посещённых
        components.push_back(vector<int>())
        dfsT(v)

Алгоритм топологической сортировки работает за $O(V+E)$, суммарное время поисков в глубину по транспонированному графу также есть $O(V+E)$, так как каждая вершина посещается ровно один раз.

Поиск мостов и компонент рёберной двусвязности

Мост (bridge) - ребро в неориентированном графе, удаление которого увеличивает количество компонент связности.

Введём на вершинах графа отношение рёберной двусвязности: $a \sim b$, если между $a$ и $b$ есть два не пересекающихся по рёбрам пути. Это отношение симметрично, рефлексивно (из вершины в неё саму есть два пути длины ноль, которые совпадают, но не пересекаются по рёбрам), а также транзитивно: пусть $a \sim b, b \sim c$, покажем, что $a \sim c$. Два не пересекающихся по рёбрам пути между $b$ и $c$ образуют цикл $C$. Тогда пусть $u, v$ - первые вершины на двух не пересекающихся по рёбрам путях из $a$ в $b$, которые лежат на цикле $C$; на цикле всегда найдутся не пересекающиеся по рёбрам пути из $u$ и $v$ в $c$.

Итак, ~ - отношение эквивалентности. Классы эквивалентности, на которые оно разбивает вершины графа, называют компонентами рёберной двусвязности (2-edge-connected components). Граф, состоящий из одной такой компоненты, называют рёберно двусвязным (2-edge-connected graph).

Множество мостов совпадает со множеством рёбер, концы которых лежат в разных компонентах рёберной двусвязности: это рёбра, которые являются единственным путём между своими концами. Отсюда также следует, что все мосты всегда входят в любой лес поиска в глубину.

Поиск мостов

Здесь и далее будем обозначать ребро дерева поиска в глубину между вершиной и и её родителем за $e_{u}$.

Как понять по ребру $e_{u}=(v, u)$ дерева поиска в глубину, является ли оно мостом? Если $e_{u}$ - мост, то из поддерева $u$ нет обратных рёбер, ведущих за пределы поддерева. Если же $e_{u}$ - не мост, то существует путь из $u$ в $v$, не проходящий по ребру $e_{u}$, то есть содержащий обратное ребро, ведущее в $v$ или её предка.

Пусть $\operatorname{low}(u)$ - минимальное время входа среди всех вершин поддерева $u$ и всех концов обратных рёбер, инцидентных вершинам этого поддерева. Тогда $e_{u}$ - мост тогда и только тогда, когда $\operatorname{low}(u)>t_{i n}(v)$. Значение $\operatorname{low}(u)$ можно вычислить во время поиска в глубину:

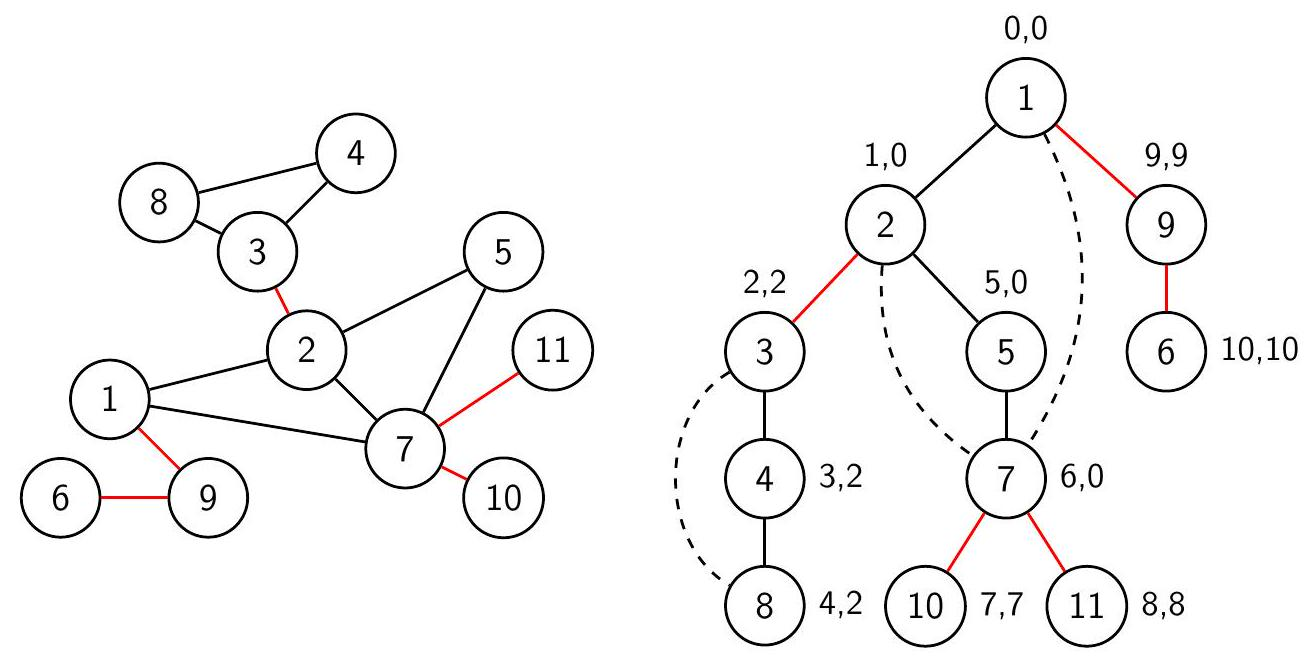
Граф и его дерево поиска в глубину с отмеченными временами входа и значениями low. Мосты помечены красным цветом. Компоненты рёберной двусвязности: $\{1,2,5,7\},\{3,4,8\},\{6\},\{9\},\{10\},\{11\}$.

Поиск компонент рёберной двусвязности

Зная мосты, несложно найти и компоненты рёберной двусвязности: компонента, содержащая корень дерева, состоит из вершин, на пути в дереве от корня до которых нет мостов; если ребро дерева $e_{u}=(v, u)$ - мост, то компонента, содержащая вершину $u$, состоит из вершин поддерева $u$, на пути от $u$ до которых нет мостов. Значит, компоненты можно найти, запуская поиски в глубину на уже построенном лесе поиска в глубину, в котором помечены мосты.

Можно найти компоненты и в процессе поиска мостов: будем складывать вершину в стек в начале её обработки. Каждый раз, когда мы находим мост $e_{u}=(v, u)$, будем доставать вершины из стека, пока не достанем $u$. При этом мы достанем вершины, лежащие в поддереве $u$, на пути в дереве от $u$ до которых не было моста (иначе мы достали бы их раньше). Значит, мы достанем ровно компоненту вершины $u$. По тем же причинам в конце в стеке останется ровно компонента корня дерева.

Получаем алгоритм поиска мостов и компонент рёберной двусвязности за $O(V+E)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

vector<vector<int> > components
vector<int> stack
T = 0
dfs(v, parent):
    visited[v] = True
    tin[v] = low[v] = T, T += 1
    stack.push_back(v)
    for u in es[v]:
        if u != parent: # проверяем, что это не ребро, по которому пришли в v;
                    # если есть кратные рёбра, нужно проверять аккуратнее
            if not visited[u]:
                dfs(u, v)
                if low[u] > tin[v]: # (v, u) - mост
                vector<int> component
                while component.size() == 0 or component.back() != u:
                    component.push_back(stack.back())
                        stack.pop_back()
                components.push_back(component)
            low[v] = min(low[v], low[u])
                else: # обратное ребро
                low[v] = min(low[v], tin[u])
fill(visited, False)
for v = 0..(n - 1):
    if not visited[v]:
        stack.clear()
        dfs(v, -1)
        components.push_back(stack) # компонента корня дерева

По любому графу можно построить лес, вершинами которого будут компоненты рёберной двусвязности графа, а рёбрами - мосты.

Поиск точек сочленения и компонент вершинной двусвязности

Точка сочленения (cut vertex, articulation point) - вершина неориентированного графа, удаление которой увеличивает количество компонент связности.

Введём на рёбрах графа отношение вершинной двусвязности: $e_{1} \sim e_{2}$, если $e_{1}=e_{2}$, или если существует простой цикл (цикл, в котором вершины не повторяются), проходящий одновременно через $e_{1}$ и $e_{2}$ (или, что то же самое, есть два не пересекающихся по вершинам пути из концов $e_{1}$ в концы $e_{2}$ ). Это отношение рефлексивно, симметрично и транзитивно: покажем, что если $e_{1} \sim e_{2}$ и $e_{2} \sim e_{3}$, то $e_{1} \sim e_{3}$. Можно считать, что $e_{1}, e_{2}, e_{3}$ попарно различны (иначе доказывать нечего). Пусть $C$ - простой цикл, проходящий через $e_{2}$ и $e_{3}$. Пусть $u, v$ - первые вершины на не пересекающихся по вершинам путях из концов $e_{1}$ в концы $e_{2}$, которые лежат на цикле $C ; u \neq v$, на цикле найдётся два не пересекающихся по вершинам пути из $u, v$ в концы $e_{3}$.

Значит, ~ - отношение эквивалентности; классы эквивалентности, на которые разбиваются рёбра, называют компонентами вершинной двусвязности, или просто компонентами двусвязности (biconnected components), а также блоками (blocks). Граф, состоящий из одной компоненты двусвязности, называют вершинно двусвязным, или просто двусвязным (biconnected graph).

Для каждой компоненты двусвязности $F$ можно рассмотреть подграф $H=(W, F)$, где $W$ - множество концов рёбер из $F$. Этот подграф тоже будем называть компонентой двусвязности или блоком. Заметим, что такой подграф всегда связен.

Любые два блока (как подграфы) либо не пересекаются по вершинам, либо пересекаются ровно по одной вершине: пусть компоненты $H_{1}, H_{2}$ пересеклись по вершинам $a \neq b$; между $a$ и $b$ есть два пути - один в $H_{1}$, другой в $H_{2}$. Объединение этих путей даёт простой цикл, на котором лежат рёбра из разных компонент двусвязности, что невозможно.

Множество вершин, лежащих в пересечении нескольких компонент двусвязности, совпадает со множеством точек сочленения: это вершины, у которых есть соседи из разных компонент двусвязности.

Рассмотрим вспомогательный граф, вершины которого - это точки сочленения и блоки, а рёбра соответствуют парам из точки сочленения и блока, в котором эта точка лежит. В этом графе нет циклов (точки сочленения на таком цикле не были бы точками сочленения). При этом если исходный граф связен, то этот граф тоже связен: в этом случае он является деревом, и его называют деревом блоков и точек сочленения (block-cut tree). В случае несвязного графа такое дерево есть у каждой компоненты связности.

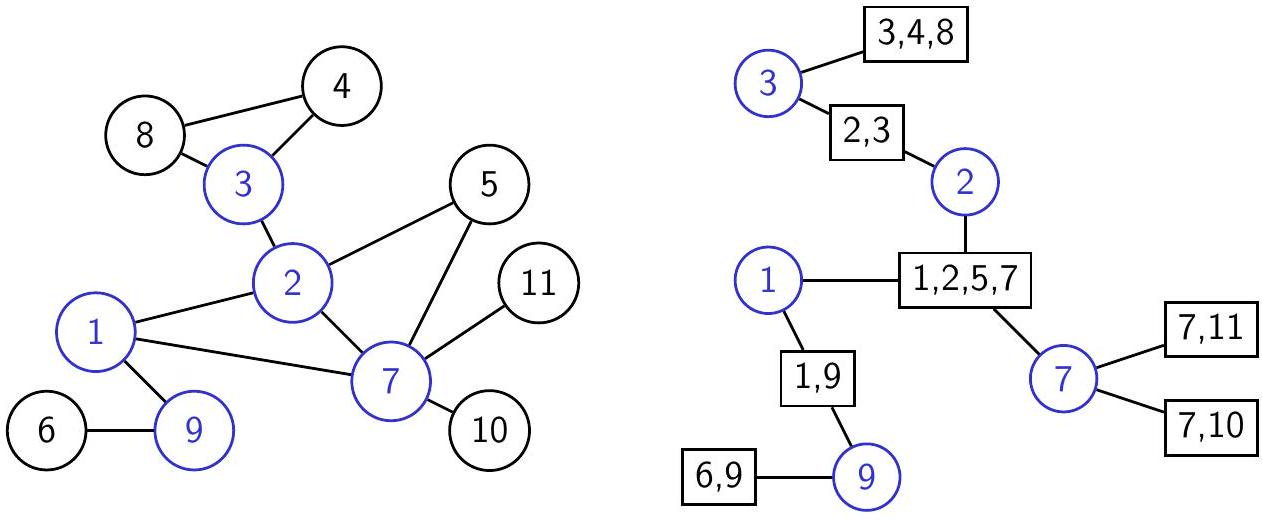
Граф и его дерево блоков и точек сочленения. Точки сочленения помечены синим цветом.

Заметим, что мосты соответствуют компонентам двусвязности, состоящим из одного ребра.

Поиск точек сочленения

Для поиска точек сочленения снова воспользуемся значениями low. Пусть $v$ - вершина, не являющаяся корнем дерева поиска в глубину. $v$ - точка сочленения тогда и только тогда, когда у вершины $v$ есть такой ребёнок $u$, что $\operatorname{low}(u) \geqslant t_{i n}(v)$ (то есть из поддерева $u$ нет обратных рёбер, ведущих за пределы поддерева $v$ ). Действительно, это условие равносильно тому, что при удалении $v$ корень и некоторая вершина $u$, соседняя с $v$, окажутся в разных компонентах связности.

Корень дерева же является точкой сочленения тогда и только тогда, когда он имеет хотя бы два ребёнка (это следует из того, что перекрёстных рёбер не бывает).

Поиск компонент двусвязности

Как найти компоненты двусвязности? Во-первых, заметим, что любое обратное ребро между вершиной $u$ и её предком $w$ лежит в той же компоненте, что и ребро дерева $e_{u}$ (они лежат на простом цикле, состоящем из пути в дереве от $w$ до $u$ и обратного ребра).

Остаётся разбить на компоненты рёбра дерева. Назовём ребро дерева $e_{u}=(v, u)$ интересным, если low $(u) \geqslant t_{i n}(v)$. В частности, все рёбра дерева между корнем и его ребенком - интересные; при поиске точек сочленения, не являющихся корнем, мы искали как раз интересные рёбра.

Заметим, что если ребро $e_{u}=(v, u)$ - не интересное, то $e_{u}$ и $e_{v}$ лежат в одной компоненте двусвязности. Если же ребро $e_{u}=(v, u)$ - интересное, то все рёбра дерева из той же компоненты двусвязности, что и $e_{u}$, находятся в поддереве вершины $u$.

Получаем следующий алгоритм: будем обходить рёбра дерева в порядке поиска в глубину, тогда ребро дерева $e_{u}=(v, u)$ либо лежит в той же компоненте, что и $e_{v}$ (если $e_{u}$ не интересное), либо лежит в новой компоненте, рёбра из которой мы до этого не встречали.

Можно строить компоненты и прямо во время поиска точек сочленения (подробности на следующей странице).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# для удобства считаем, что граф простой (если это не так, некоторые проверки
# нужно проводить аккуратнее, а в стеке нужно различать кратные рёбра)
vector<vector<pair<int, int> > > components
vector<pair<int, int> > stack
T = 0
dfs(v, parent):
    visited[v] = True
    tin[v] = low[v] = T, T += 1
    count = 0 # считаем количество детей
    for u in es[v]:
        if u != parent: # проверяем, что это не ребро, по которому пришли в V
            if not visited[u] or tin[u] < tin[v]: # видим ребро в первый раз
                stack.push_back({v,u})
            if not visited[u]:
                count += 1
                dfs(u, v)
                if low[u] >= tin[v]: # (v, u) - интересное
                    vector<pair<int, int> > component
                    while component.size() == 0 or component.back() != {v,u}:
                        component.push_back(stack.back())
                        stack.pop_back()
                    components.push_back(component)
                    if parent != -1 or count >= 2:
                    ... # v - точка сочленения
                low[v] = min(low[v], low[u])
            else: # oбратноe pe6po
                low[v] = min(low[v], tin[u])
fill(visited, False)
for v = 0..(n - 1):
    if not visited[v]:
            dfs(v, -1)

Будем класть ребро в стек, когда видим его в первый раз (в простом графе это равносильно тому, что ребро ведёт в непосещённую вершину, либо в вершину с меньшим временем входа, чем у текущей). Каждый раз, когда мы находим интересное ребро дерева $e_{u}=(v, u)$, будем доставать рёбра из стека, пока не достанем $e_{u}$. При этом любое обратное ребро $(a, b)$ ( $a$ - потомок $b$ ) мы достанем одновременно с ребром $e_{a}$ (и они действительно должны лежать в одной компоненте). Что касается рёбер дерева, мы достанем все рёбра из поддерева $u$, которые не интересные сами, и на пути от которых до $e_{u}$ нет других интересных рёбер (все остальные мы достали раньше). Это ровно те рёбра дерева, которые лежат в одной компоненте с $e_{u}$. Поскольку все рёбра из корня в его детей - интересные, по завершении обработки корня стек будет пустой.

Получаем алгоритм поиска точек сочленения и компонент двусвязности за $O(V+E)$.

2-SAT

Булева переменная (boolean variable) - переменная, принимающая одно из двух значений: истина или ложь; true или false; 1 или 0. Литерал (literal) - это булева переменная или её отрицание. Если $x$ - булева переменная, то $x, \neg x$ (так обозначается отрицание) литералы.

Конъюнктивная нормальная форма (KHФ, conjunctive normal form, CNF) представляет собой конъюнкцию (conjunction), то есть логическое “И”, нескольких дизъюнктов. Каждый дизъюнкт (clause) представляет собой дизъюнкцию (disjunction), то есть логическое “ИЛИ”, нескольких литералов. Пример КНФ от переменных $x_{1}, x_{2}, x_{3}, x_{4}$ (конъюнкция обозначается как $\wedge$, дизъюнкция - как $\vee$ ):

Дизъюнкт называется выполненным (satisfied), если хотя бы один его литерал имеет значение true. KHФ выполнима (satisfiable), если существует набор значений переменных, при котором выполнены все дизъюнкты. Такой набор значений называют выполняющим набором. Один из выполняющих наборов для формулы выше - true,false,true,false.

В 2-KHФ каждый дизъюнкт состоит из двух литералов. Задача 2-SAT (2-satisfiability) формулируется следующим образом: дана 2-КНФ; нужно проверить, выполнима ли она, и предъявить выполняющий набор, если он существует. Примеры 2-KНФ:

выполнима (выполняющий набор - true,false,false,true);

невыполнима.

Решение задачи 2-SAT

Пусть дана 2-КНФ $A$ на $n$ переменных $x_{1}, \ldots, x_{n}$, состоящая из $m$ дизъюнктов. Построим по ней граф импликаций $G_{A}$. Вершинами этого графа будут все $2 n$ литералов. Для каждого дизъюнкта ( $a \vee b$ ) ( $a, b$ - литералы) проведём два ребра: $\neg a \rightarrow b$ и $\neg b \rightarrow a$ (если $a=\neg x_{i}$, то $\left.\neg a=\neg\left(\neg x_{i}\right)=x_{i}\right)$.

Заметим, что дизъюнкт ( $a \vee b$ ) эквивалентен любой из двух импликаций (implications, “если…, то…”) $\neg a \Rightarrow b$ и $\neg b \Rightarrow a$. Таким образом, для любого пути в графе импликаций из $c$ в $d$ и значений $c, d$ из любого выполняющего набора верно, что $c \Rightarrow d$.

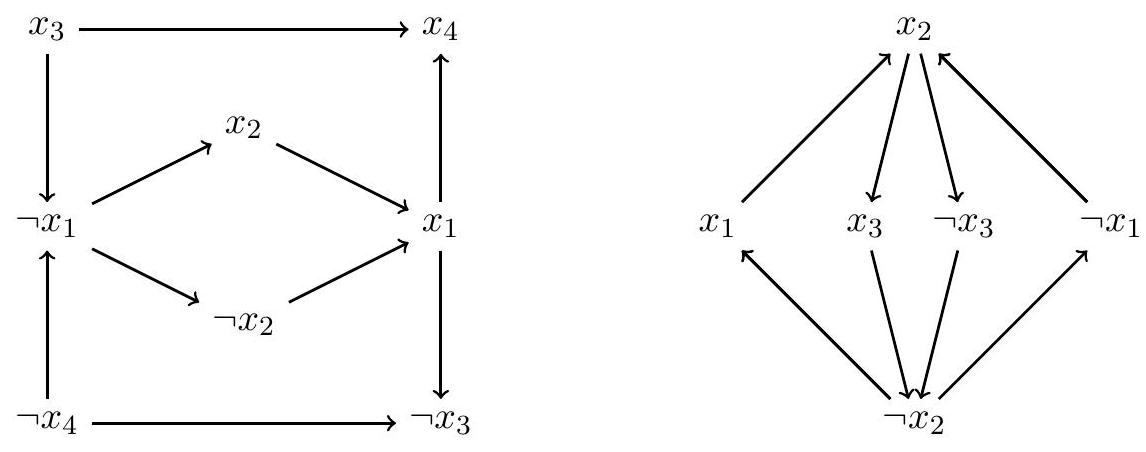
Графы импликаций 2-КНФ из примеров выше

Если для какой-то переменной $x_{i}$ литералы $x_{i}$ и $\neg x_{i}$ оказались в одной компоненте сильной связности графа импликаций, то $A$ невыполнима. Действительно, если бы нашёлся выполняющий набор, для него было бы верно одновременно $x_{i} \Rightarrow \neg x_{i}$ и $\neg x_{i} \Rightarrow x_{i}$. Но если $x_{i}$ равно true, то неверна первая импликация, а если $x_{i}$ равно false, то вторая.

Пусть это не так, то есть никакая компонента сильной связности не содержит одновременно литерал и его отрицание. Тогда построим выполняющий набор следующим образом: пронумеруем компоненты сильной связности в порядке топологической сортировки (алгоритм нахождения компонент сильной связности находит их именно в таком порядке); пусть $k[a]$ - номер компоненты литерала $a . k\left[x_{i}\right] \neq k\left[\neg x_{i}\right]$ для любой переменной $x_{i}$; присвоим переменной $x_{i}$ значение true, если $k\left[x_{i}\right]>k\left[\neg x_{i}\right]$, и значение false иначе.

Почему получился выполняющий набор? Пусть нашёлся невыполненный дизъюнкт $(a \vee b)(a, b-$ литералы). В графе импликаций ему соответствуют рёбра $\neg a \rightarrow b$ и $\neg b \rightarrow a$, откуда следует $k[b] \geqslant k[\neg a], k[a] \geqslant k[\neg b]$. С другой стороны, из того, что дизъюнкт невыполнен, следует, что $k[\neg a]>k[a], k[\neg b]>k[b]$. Получаем $k[b] \geqslant k[\neg a]>k[a] \geqslant k[\neg b]>k[b]$, что невозможно.

Таким образом, получаем следующий алгоритм: строим граф импликаций; находим его компоненты сильной связности и значения $k$ для всех вершин графа; проверяем, верно ли, что $k\left[x_{i}\right] \neq k\left[\neg x_{i}\right]$ для всех переменных. Если это не так, то $A$ невыполнима; если это так, то выполняющий набор строится следующим образом: присвоим true всем $x_{i}$ таким, что $k\left[x_{i}\right]>k\left[\neg x_{i}\right]$, остальным присвоим f alse.

Поскольку в графе импликаций $2 n$ вершин и $2 m$ рёбер, время работы алгоритма $O(n+m)$.