4. Базовые структуры данных

Массив

Массив (array) - структура данных, позволяющая хранить набор значений в ячейках, пронумерованных индексами (или набором индексов в случае многомерного массива) из некоторого отрезка целых чисел. Встроен в большинство современных языков программирования.

Массив позволяет за константное $(O(1))$ время получать доступ к элементу по индексу, а также изменять этот элемент. При этом массив имеет фиксированный размер, поэтому не поддерживает операций вставки и удаления элементов. Если хочется вставить или удалить элемент, можно создать новый массив нужного размера и скопировать информацию в него, но это потребует $\Theta(n)$ операций, где $n$ - длина массива.

Поиск элемента в массиве по значению также имеет сложность $\Theta(n)$, так как нужно проверить все элементы массива. Если массив специально упорядочен (например, элементы массива расположены в возрастающем порядке), то поиск можно делать быстрее (скоро мы изучим алгоритм двоичного поиска).

Немного о работе с массивом в C++:

int a[n]; // объявить массив длины n, нумерация ячеек от 0 до n-1
a[i]; // обращение к i-му элементу массива
a[i] = x; // присвоить x в i-ю ячейку массива
int b[n][m]; // объявить двумерный массив, нумерация ячеек двумя индексами,
    // от 0 до n-1 и от 0 до m-1
b[i][j]; // обращение к j-му элементу i-й строки массива
b[i][j] = y; // присвоение

Связный список

Связный список (linked list) состоит из узлов, каждый из которых содержит данные и ссылки на соседние узлы. 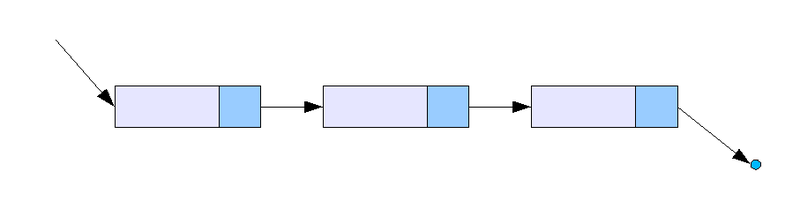В двусвязном списке поддерживаются ссылки на следующий и предыдущий узел, в односвязном списке - только на следующий. 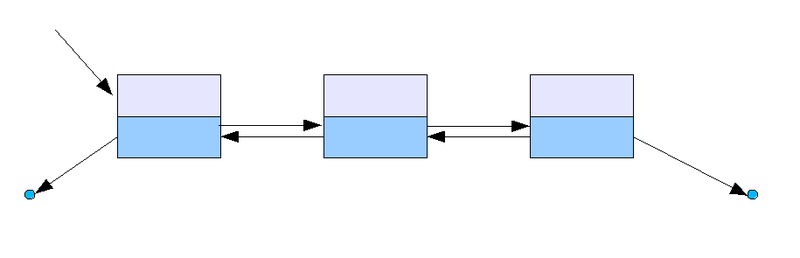Также поддерживаются ссылки на начало и конец списка (их часто называют головой и хвостом). Для того, чтобы посетить все узлы, можно начать с головы и переходить по ссылке на следующий узел, пока он существует.

Преимущество списка перед массивом - возможность вставлять и удалять элементы за $O(1)$.

Недостаток списка - невозможность быстрого доступа к произвольному элементу. Так, доступ к $i$-му элементу можно получить, лишь $i$ раз пройдя по ссылке вперёд, начиная из головы списка (то есть за $\Theta(i)$ ).

Удобно делать голову и хвост фиктивными элементами и не хранить в них никаких данных, тогда функции вставки и удаления элементов пишутся проще.

Примерная реализация двусвязного списка на C++:

struct Node { // один узел списка
    Node *next, *prev; // указатели на следующий и предыдущий узлы
    int x; // данные, хранящиеся в узле
};
struct List {
    Node *head, *tail; // указатели на начало и конец списка
    List() { // инициализируем пустой список - создаём фиктивные head и tail
                // и связываем их друг с другом
        head = new Node();
        tail = new Node();
        head->next = tail;
        tail->prev = head;
    }
    void pushBack(int x) { // вставить x в конец списка
        Node *v = new Node();
        v->x = x, v->prev = tail->prev, v->next = tail;
        v->prev->next = v, tail->prev = v;
    }
    void insert(Node *v, int x) { // вставить x после v
        Nove *w = new Node();
        w->x = x, w->next = v->next, w->prev = v;
        v->next = w, w->next->prev = w;
    }
    void erase(Node *v) { // удалить узел v
        v->prev->next = v->next;
        v->next->prev = v->prev;
        delete v;
    }
    Node *find(int x) { // найти x в списке
        for (Node *v = head->next; v != tail; v = v->next) {
            if (v->x == x) {
                return v;
            }
        }
        return nullptr;
    }
};

Можно хранить узлы списка в массиве, тогда вместо указателей можно использовать числа - номера ячеек массива. Но тогда нужно либо заранее знать количество элементов в списке, либо использовать динамический массив (который мы скоро изучим).

Можно также использовать встроенный в C++ двусвязный список - std::list. Односвязный список использует меньше дополнительной памяти, но не позволяет перемещаться по списку в сторону начала. Также из него сложнее удалять элементы - не получится удалить элемент, имея ссылку только на него. Нужно как-то получить доступ к предыдущему элементу, чтобы пересчитать ссылку из него на следующий.

Динамический массив

Пусть мы хотим научиться вставлять новые элементы в конец массива. Можно попытаться сразу создать массив достаточно большого размера, и в отдельной переменной поддер-

живать его реальную длину. Но далеко не всегда максимальное количество элементов известно заранее.

Поступим следующим образом: если мы хотим вставить новый элемент, а место в массиве закончилось, то создадим новый массив вдвое большего размера, и скопируем данные туда.

int *a; // используемая память
int size; // размер памяти
int n; // реальный размер массива
void pushBack(int x) { // вставить х в конец массива
    if (n == size) {
        int *b = new int[size * 2];
        for (int i = 0; i < size; ++i) {
            b[i] = a[i];
        }
        delete[] a;
        a = b;
        size *= 2;
    }
    a[n] = x;
    n += 1;
}
void popBack() { // удалить последний элемент
    n -= 1;
}

В C++ можно и нужно использовать встроенную реализацию динамического массива std::vector.

Каждая конкретная операция вставки элемента может работать долго $-\Theta(n)$, где $n$ - длина массива. Зато можно показать, что среднее время работы операции вставки $O(1)$. Докажем этот факт при помощи метода амортизационного анализа, который нам ещё не раз пригодится.

Это утверждение равносильно тому, что суммарное время работы $m$ операций вставки - $O(m)$.

Стек, очередь, дек

Стек (stack) позволяет поддерживать список элементов, вставлять элемент в конец списка, а также удалять элемент из конца списка. Часто также говорят, что он организован по принципу LIFO (last in - first out).

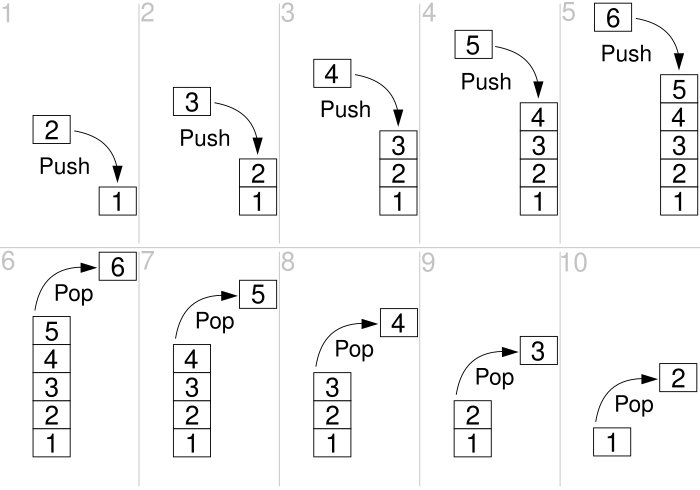
Очередь (queue) организована по принципу FIFO (first in - first out). Она позволяет вставлять элемент в конец списка, а также удалять элемент из начала списка.

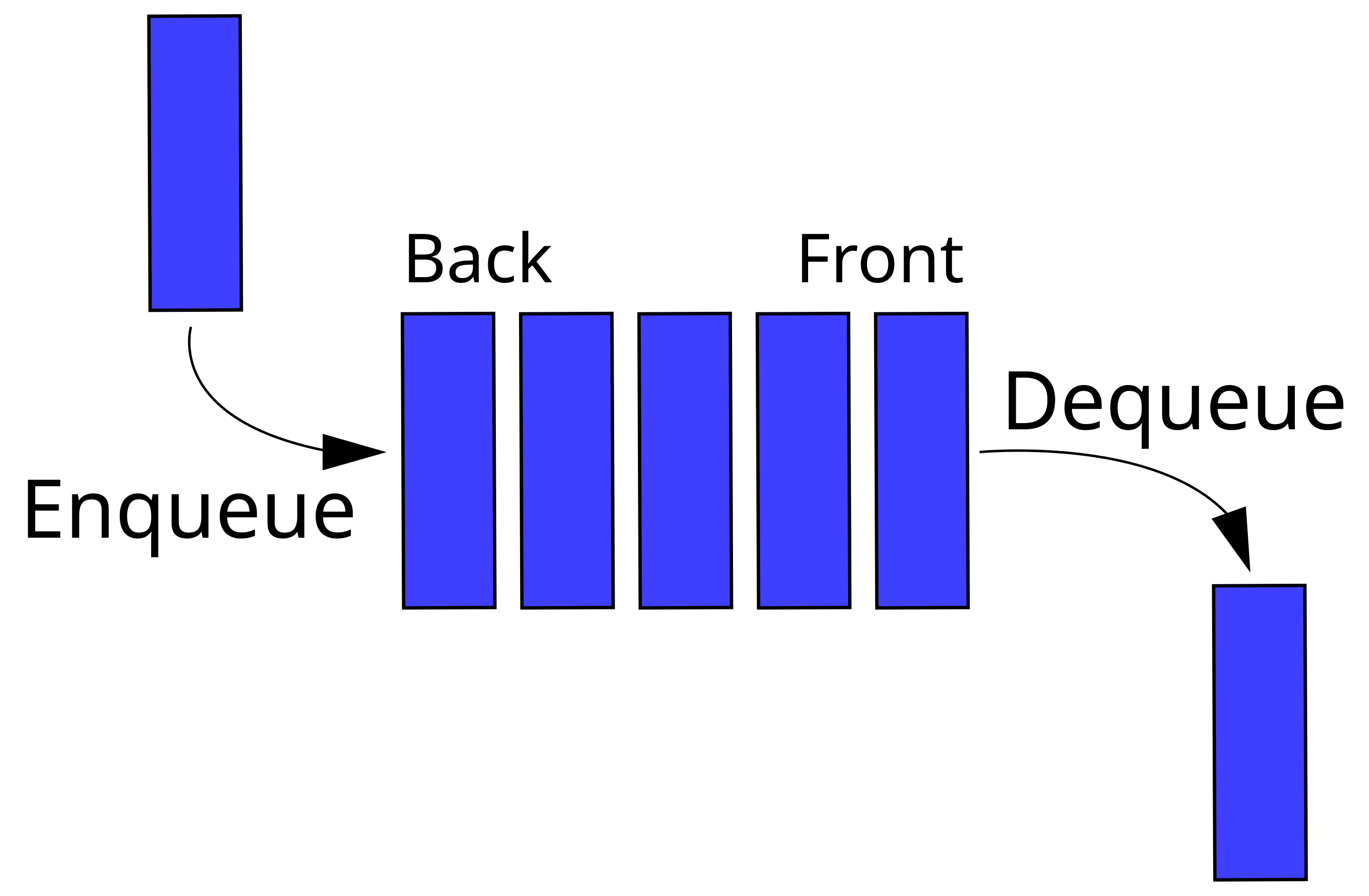
Дек (deque - double ended queue), или двусторонняя очередь, отличается от обычной очереди тем, что позволяет добавлять и удалять элементы как в начало, так и в конец списка.

Все эти структуры можно реализовать с помощью связного списка. Для стека и очереди хватит односвязного списка: в стеке достаточно поддерживать ссылку на предыдущий элемент, а в очереди - на следующий. Для реализации дека понадобится двусвязный список.

Также все три структуры можно реализовать с помощью динамического массива. В случае дека нужно научиться добавлять элементы в начало, для чего можно зациклить массив. То же самое можно сделать в реализации очереди, чтобы переиспользовать освободившееся место в начале массива. Приведём примерную реализацию дека на динамическом массиве:

int *a; // используемая память
int size; // размер памяти
int b, e; // дек использует ячейки в диапазоне [b,e), или,
    // если b >= e, в диапазонах [b,size) и [0,e)
int getSize() { // узнать количество элементов в деке
    if (b < e) {
        return e - b;
    } else {
        return e - b + size;
    }
}
void pushBack(int x) { // вставить x в конец дека
    if (getSize() == size) {
        ... // выделяем вдвое больше памяти
    }
    a[e] = x;
    e = (e + 1) % size;
}
void popBack() { // удалить элемент из конца дека
    e = (e - 1 + size) % size;
}
void pushFront(int x) { // вставить x в начало дека
    if (getSize() == size) {
        ... // выделяем вдвое больше памяти
    }
    a[b] = x;
    b = (b - 1 + size) % size;
}
void popFront() { // удалить элемент из начала дека
    b = (b + 1) % size;
}

В C++ существуют встроенные реализации этих структур - std::stack, std::queue, std::deque.