12. Графы. Определения и способы хранения

Определения

Граф задаётся множеством вершин $V$ и множеством рёбер $E$, соединяющих пары вершин (в английском языке граф - graph, вершина - vertex или node, ребро - edge).

В ориентированном (directed graph, digraph) графе каждое ребро имеет направление, то есть является упорядоченной парой вершин (может быть ребро из вершины $a$ в вершину $b$, но не быть ребра из $b$ в $a$ ). В неориентированном (undirected) графе рёбра направлений не имеют, то есть являются неупорядоченными парами (считаем, что ребро, ведущее из $a$ в $b$, ведёт и из $b$ в $a$ тоже).

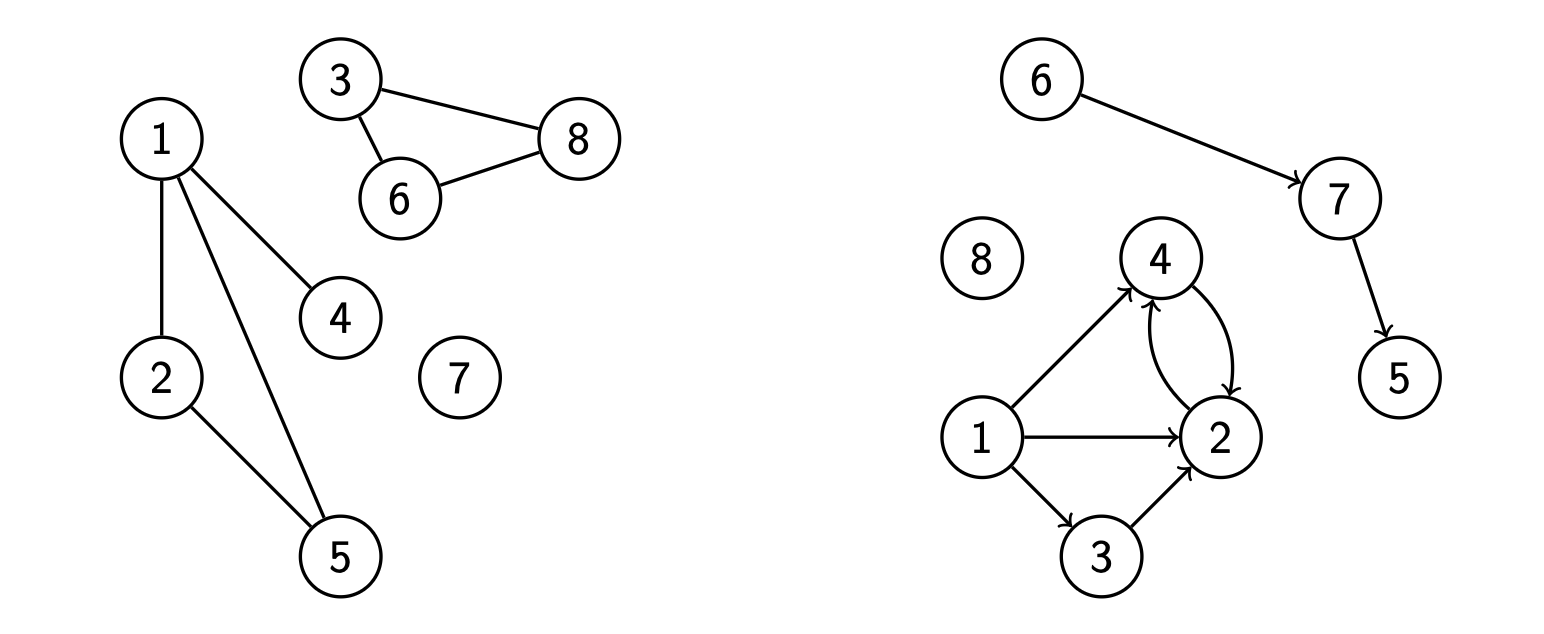
Неориентированный и ориентированный графы

Пример неориентированного графа - карта стран (вершины - страны, рёбра есть между странами, имеющими общую границу). Пример ориентированного графа - интернет (вершины - сайты, рёбра - гиперссылки). Ещё примеры графов - транспортные сети (автомобильные, железнодорожные, авиационные), графы друзей в соцсетях.

В графе может быть несколько рёбер между одной парой вершин (несколько рёбер в одном направлении в ориентированном графе). Такие рёбра называются кратными (multiple edges). Ребро, концы которого совпадают, называют петлёй (loор). Графы без петель и кратных рёбер называют простыми (simple).

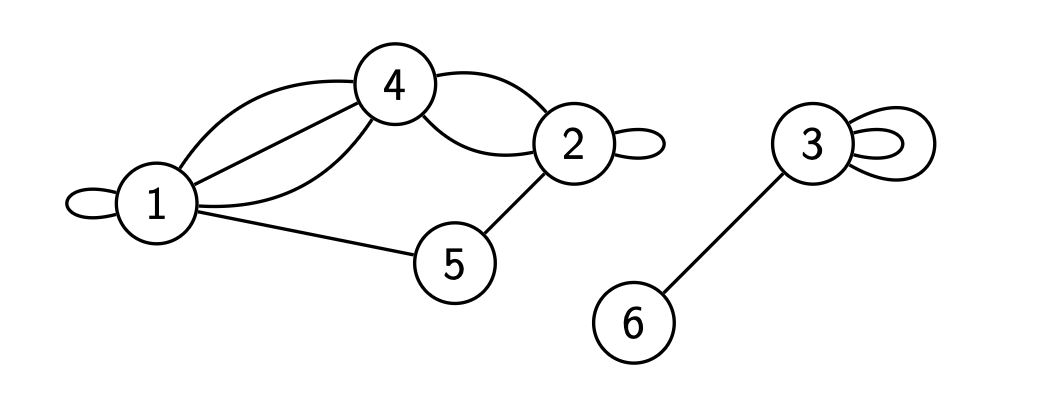
Граф с петлями и кратными рёбрами

Для ребра $e=(a, b)$ вершины $a$ и $b$ называют его концами (endpoints) (или началом и концом в случае ориентированного графа). Ребро инцидентно (incident) каждому из

своих концов. Две вершины неориентированного графа, соединённые ребром, называют смежными (adjacent). Два ребра неориентированного графа, имеющие общий конец, тоже называют смежными.

Степень (degree) вершины неориентированного графа $\operatorname{deg}(v)$ - это количество инцидентных ей рёбер (при этом каждая петля считается два раза). В ориентированном графе у вершины $v$ есть входящая степень (indegree) $\operatorname{deg}_{i n}(v)$ - количество рёбер, входящих в $v$, и исходящая степень (outdegree) $\operatorname{deg}_{\text {out }}(v)$ - количество рёбер, исходящих из $v$.

Подграф (subgraph) $H=(W, F)$ графа $G=(V, E)$ - это граф на подмножестве вершин $W \subseteq V$ и подмножестве рёбер $F \subseteq E$ графа $G$, так что оба конца любого ребра из $F$ лежат в $W$. Индуцированный подграф (induced subgraph) $H=(W, F)$ содержит все рёбра исходного графа, оба конца которых лежат в $W$. Остовный подграф (spanning subgraph) содержит все вершины исходного графа ( $W=V$ ), но не обязательно все рёбра.

Способы хранения графа

Чаще всего граф хранят одним из следующих двух способов (считаем, что $|V|=n$, $\left.V=\left\{v_{0}, \ldots, v_{n-1}\right\}\right)$ :

  • Матрица смежности (adjacency matrix) графа - это матрица (двумерный массив) $a$ размера $n \times n$, где $a_{i, j}$ - количество рёбер, идущих из $v_{i}$ в $v_{j}$. Матрица смежности простого графа состоит из нулей и единиц, а её главная диагональ (множество элементов вида $a_{i, i}$ ) состоит из нулей. Матрица смежности неориентированного графа симметрична ( $a_{i, j}=a_{j, i}$ ).
  • Списки смежности (adjacency lists) графа - это набор списков, по одному для каждой вершины: в списке смежности вершины $v$ хранится список вершин, в которые ведут рёбра из $v$ (или список самих рёбер). В графе с кратными рёбрами вершина $u$ встречается в списке $v$ столько раз, сколько рёбер из $v$ в $u$ есть в графе. В неориентированном графе каждое ребро входит в списки обоих своих концов; в ориентированном - только в список своего начала. Размер списка смежности вершины $v$ равен $\operatorname{deg}(v)\left(\operatorname{deg}_{\text {out }}(v)\right.$ в ориентированном графе).

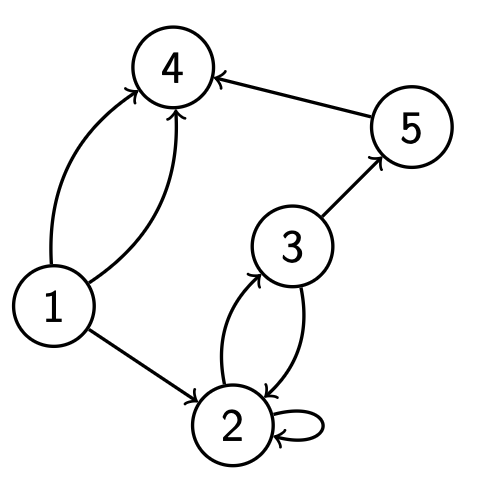
$$ \begin{pmatrix} 0 & 1 & 0 & 2 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix} \qquad \begin{array}{cl} 1 & \to 2, 4, 4 \\ 2 & \to 2, 3 \\ 3 & \to 2, 5 \\ 4 & \to \varnothing \\ 5 & \to 4 \\ \end{array} $$

Матрица смежности позволяет для любой пары вершин за $O(1)$ проверить, соединены ли эти вершины ребром. Однако она занимает $O\left(n^{2}\right)=O\left(V^{2}\right)$ памяти (здесь и далее для краткости в асимптотических оценках вместо $|V|,|E|$ будем писать просто $V, E)$. Если хочется проверять наличие ребра за $O(1)$, используя меньше памяти, можно вместо всей матрицы смежности хранить в хеш-таблице пары вершин, связанных ребром.

Списки смежности можно реализовывать как динамическими массивами, так и связными списками. В любом случае, они занимают суммарно $O(V+E)$ памяти, и позволяют для любой вершины быстро просмотреть всех её соседей. Проверка наличия ребра между парой вершин $u, v$ при использовании только списка смежности займёт $O(\min (\operatorname{deg}(u), \operatorname{deg}(v)))$ ( $\operatorname{deg}_{\text {out }}$ в ориентированном графе).