15. Жадные алгоритмы

Алгоритм Хаффмана

Алгоритм Хаффмана (Huffman, 1952) - один из самых известных алгоритмов сжатия текста. Пусть дан текст, состоящий из символов алфавита $\Sigma$, который мы хотим закодировать как можно более короткой последовательностью бит.

Префиксные коды

Самый простой способ - кодировать каждый символ уникальной последовательностью из $k$ бит (будем называть такую последовательность кодовым словом (codeword)), где $2^{k} \geqslant|\Sigma|$ (чтобы такое кодирование вообще было возможно). Такой способ не всегда эффективен: например, пусть $\Sigma=\{a, b, c, d\}$, текст имеет длину 10000 , но большая часть символов текста равна $a$ (скажем, $a$ встречается в тексте 7000 раз, а остальные символы по 1000 раз). Тогда вышеописанный способ кодирования потребует $20000$ бит. Если же кодовое слово символа $а$ будет равно $0$ , символа $b-10, c-110, d-111$, то суммарно потребуется лишь $7000 \cdot 1+1000 \cdot 2+1000 \cdot 3+1000 \cdot 3=15000$ бит.

Итак, иногда оказывается выгодным использовать кодовые слова разной длины для разных символов. Заметим, что при этом нельзя использовать одновременно кодовые слова, одно из которых является префиксом другого: в этом случае нельзя будет понять, где в закодированной последовательности бит заканчивается одно кодовое слово, и начинается следующее. Коды, в которых ни одно кодовое слово не является префиксом другого, называют префиксными (prefix codes) (логичнее было бы называть их беспрефиксными, но термин “префиксный код” является общепринятым).

Какой префиксный код будет оптимальным для данного текста $t$ ? Пусть $\operatorname{cnt}(t, a)$ количество вхождений символа $a$ в текст (будем называть это количество частотой), $l e n(C, a)$ - длина кодового слова символа $a$ в префиксном коде $C$. Тогда количество бит, которое понадобится для того, чтобы закодировать текст $t$ кодом $C$, равняется

$$ L(C, t)=\sum_{a} c n t(t, a) \cdot \operatorname{len}(C, a) . $$

Мы хотим найти префиксный код $C$, минимизирующий $L(C, t)$.

Связь с двоичными деревьями

Любому префиксному коду можно сопоставить двоичное дерево: кодовые слова будут соответствовать листьям дерева; для того, чтобы по листу получить кодовое слово, нужно пройти по пути из корня в этот лист, и выписывать 0 при спуске в левого ребёнка, 1 при спуске в правого.

В дереве оптимального префиксного кода ни у какой вершины не может быть ровно один ребенок: такую вершину можно просто удалить, поставив её ребёнка на её место; при этом новое дерево будет всё ещё соответствовать префиксному коду, но длина некоторых кодовых слов уменьшится.

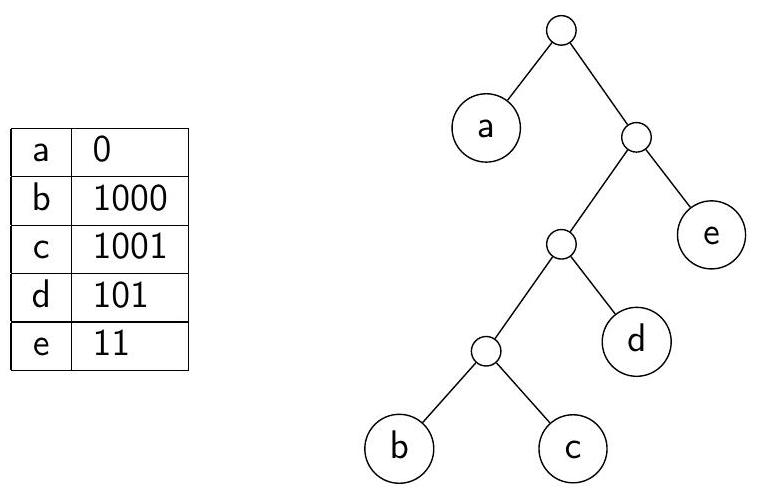
Префиксный код и соответствующее ему двоичное дерево

Жадный алгоритм

Посмотрим на самый глубокий лист $v$ в дереве оптимального префиксного кода. У родителя $v$ есть ещё один ребёнок; обозначим его за $u$. Пути от корня до $v$ и $u$ являются кодовыми словами каких-то двух символов. Если это не два самых редко встречающихся в тексте $t$ символа, то поменяем их местами с самыми редкими. При этом длина закодированного текста может только уменьшиться. Значит, всегда найдётся оптимальный префиксный код, в дереве которого два самых редких символа находятся в соседних листьях на максимальной глубине.

Пусть $C$ - такой оптимальный код, $a$ и $b$ - два самых редких символа в $t$; они находятся в листьях $v, u$ с общим родителем $w$. Введём новый символ $c$ и рассмотрим текст $t_{1}$, полученный из $t$ заменой всех вхождений $a$ и $b$ на $c$. Также рассмотрим префиксный код $C_{1}$, соответствующий дереву кода $C$, из которого удалили $v$ и $u$, а в ставшую листом вершину $w$ поместили символ $c$. Заметим, что $L(C, t)=L\left(C_{1}, t_{1}\right)+\operatorname{cnt}(t, a)+c n t(t, b)$.

$$ L(D, t)=L\left(D_{1}, t_{1}\right)+\operatorname{cnt}(t, a)+\operatorname{cnt}(t, b) < L\left(C_{1}, t_{1}\right)+c n t(t, a)+\operatorname{cnt}(t, b)=L(C, t) . $$

Но это противоречит оптимальности $C$, значит такого $D_{1}$ не существует, и $C_{1}$ - оптимален. Кроме того, по любому оптимальному коду для $t_{1}$ вышеописанной операцией мы можем построить оптимальный код для $t$.

Будем применять эти рассуждения рекурсивно, и получать строки, в которых всё меньше и меньше различных символов. В конце концов мы получим строку, в которой встречается всего два различных символа. Оптимальный префиксный код для такой строки кодирует каждый символ одним битом.

Реализация

Будем хранить символы в очереди с приоритетами: приоритет символа равен его частоте. Пока в очереди больше одного символа, будем доставать из очереди два символа $a, b$ с минимальными приоритетами $c n t_{a}, c n t_{b}$, и складывать в очередь новый символ $c$ с приоритетом $c n t_{c}=c n t_{a}+c n t_{b}$. В этот момент будем подвешивать вершины, соответствующие символам $a$ и $b$, детьми к вершине, соответствующей символу $c$. В конце в очереди останется только один символ; вершина, соответствующая этому символу, будет корнем дерева оптимального префиксного кода. Получаем время работы $O(|\Sigma| \log |\Sigma|)$ (если считать, что частоты символов уже предподсчитаны).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


# для удобства считаем, что символы - числа от 0 до n - 1
for i = 0..(n - 1):
    q <-- (i, cnt[i]) # кладём в очередь i с приоритетом cnt[i]
for c = n..(2 * n - 2): # n - 1 итерация
    a <-- q, b <-- q # извлекаем два элемента с минимальными приоритетами
    cnt[c] = cnt[a] + cnt[b]
    v[c]->1 = v[a], v[c]->r = v[b] # подвешиваем a и b детьми к c
    q <-- (c, cnt[c])
r <-- q
return v[r] # возвращаем корень дерева

✍️ Для того, чтобы закодированный текст можно было потом раскодировать, необходимо вместе с ним в каком-то виде хранить дерево префиксного кода или таблицу частот, по которой дерево можно будет построить заново.

Оптимальное кэширование

Под кэшированием (caching) обычно имеют в виду хранение малого количества данных в быстрой памяти, производимое для того, чтобы реже взаимодействовать с медленной памятью. В современных компьютерах кэширование происходит одновременно на многих уровнях: есть кэш процессора, более медленная оперативная память, ещё более медленный жёсткий диск. Сам жёсткий диск используется браузерами для кэширования часто посещаемых веб-страниц: чтение с диска быстрее, чем их повторная загрузка из интернета.

Кэширование тем эффективнее, чем чаще оказывается, что запрашиваемые данные уже находятся в кэше. Алгоритм управления кэшом определяет, какую информацию хранить в кэше, и какую информацию удалять из него, если требуется записать в кэш новые данные.

Сформулируем задачу в абстрактном виде: есть множество из $n$ фрагментов данных, хранящихся в основной памяти. Более быстрая кэш-память способна хранить $k < n$ фрагментов данных; можно считать, что в начале работы алгоритма кэш пустой, либо что он уже содержит какие-то $k$ элементов (дальнейшие рассуждения от этого не зависят). Нужно обработать последовательность обращений к памяти $d_{1}, \ldots, d_{m}$; алгоритм должен постоянно принимать решение о том, какие элементы хранить в кэше. Запрашиваемый элемент $d_{i}$ читается очень быстро, если он уже находится в кэше. В противном случае его нужно скопировать в кэш из основной памяти; при этом, если кэш заполнен, нужно предварительно удалить из кэша какой-то другой элемент. Такая ситуация называется кэш-промахом (cache miss). Требуется минимизировать количество операций записи в кэш при обработке последовательности запросов к памяти.

Заметим, что, вообще говоря, количество операций записи в кэш может не совпадать с количеством кэш-промахов: алгоритм управления кэшом мог бы записывать в кэш элементы, которые понадобятся не прямо сейчас, а когда-нибудь потом. Поймём, почему такие действия бессмысленны: пусть в какой-то момент алгоритм записывает в кэш элемент $x$; если $x$ ни разу не будет запрошен до момента его удаления из кэша (или до конца работы алгоритма), то эту запись можно было просто не производить. Если же $x$ будет запрошен позже, то эту запись можно отложить непосредственно до момента, когда он будет запрошен: ячейка кэш-памяти, которую он занимает, всё равно до этого момента не будет никак использоваться.

Таким образом, по любому алгоритму мы можем построить его “ленивую” версию, которая записывает элемент в кэш, только если сразу после этого он будет запрошен. При этом она делает не больше операций записи в кэш, чем исходный алгоритм; количество операций записи в кэш для неё совпадает с количеством кэш-промахов.

✍️ Конечно, на практике алгоритм управления кэшом не обладает информацией о будущих запросах. Тем не менее, обладая этой информацией, можно решить задачу оптимально и получить теоретически минимально возможное количество промахов для данной последовательности запросов. Таким образом, алгоритм, который мы сейчас изучим, используется для оценки качества применяемых на практике алгоритмов.

Алгоритм Белади

Алгоритм Белади (Bélády, 1966) следует следующему правилу: когда нужно записать в кэш элемент $d_{i}$, и свободного места в кэше нет, он удаляет из кэша элемент, который понадобится в следующий раз позже всех остальных.

Обозначим алгоритм Белади за $B$. Почему $B$ оптимален? Заметим, что $B$ - ленивый. Пусть $S_{0}$ - ленивый алгоритм, делающий минимально возможное количество кэш-промахов на последовательности запросов $d_{1}, \ldots, d_{m}$. Для каждого $1 \leqslant i \leqslant m$ построим $S_{i}$ - ленивый алгоритм, делающий не больше промахов, чем $S_{0}$, и при этом при обработке первых $i$ запросов делающий те же действия, что и $B$. Тогда $S_{m}$ делает то же количество промахов, что и $B$, а значит, $B$ делает не больше промахов, чем $S_{0}$.

Пусть $1 \leqslant i \leqslant m, S_{i-1}$ уже построен. При обработке первых $i-1$ запросов $B$ и $S_{i-1}$ делали одни и те же действия, в частности, к моменту обработки $i$-го запроса содержимое кэша для этих алгоритмов совпадает. Если $d_{i}$ уже находится в кэше, или если $B$ и $S_{i-1}$ при записи $d_{i}$ в кэш удаляют из кэша один и тот же элемент, можно взять $S_{i}=S_{i-1}$.

Пусть при записи $d_{i}$ в кэш $S_{i-1}$ удаляет из кэша элемент $a$, а $B$ - элемент $b \neq a$. Заметим, что $a$ будет запрошен раньше, чем $b$ (либо они оба больше не будут запрошены). Определим $S_{i}$ следующим образом: при обработке первых $i-1$ запросов он ведёт себя как $S_{i-1}$ и $B$; при обработке $i$-го запроса оне ведёт себя как $B$, то есть удаляет из кэша $b$ и записывает на его место $d_{i}$. Далее он ведёт себя как $S_{i-1}$, пока не произойдёт одно из двух событий:

$S_{i-1}$ удаляет $b$ из кэша, и записывает на его место запрошенный элемент $d_{j}$. В этот момент $S_{i}$ запишет $d_{j}$ в кэш на место $a$; после этого содержимое кэша для $S_{i-1}$ и $S_{i}$ совпадает, поэтому дальше $S_{i}$ просто повторяет те же действия, что и $S_{i-1}$.
Запрашивается элемент $d_{j}=a$, и $S_{i}$ удаляет из кэша элемент $x$, чтобы записать на его место $a$. Если $x=b$, то $S_{i-1}$ никак не меняет кэш; если $x \neq b$, то $S_{i-1}$ удаляет $x$, и записывает на его место $b$. В любом случае, после этого содержимое кэша для $S_{i-1}$ и $S_{i}$ совпадает, поэтому дальше $S_{i}$ ведёт себя, как $S_{i-1}$. Здесь есть тонкость: в случае $x \neq b$ алгоритм $S_{i}$ ведёт себя не лениво, так как он записывает в кэш $b$ перед запросом $d_{j}=a \neq b$. Однако такой $S_{i-1}$ можно сделать ленивым, не увеличивая количество операций записи в кэш; переобозначим за $S_{i}$ его ленивую версию. В любом из вышеописанных случаев полученный алгоритм $S_{i}$ является ленивым и делает не больше кэш-промахов, чем $S_{i-1}$, то есть не больше, чем $S_{0}$.

✍️ Многие используемые на практике алгоритмы кэширования основаны на принципе LRU (least recently used): из кэша удаляется элемент, который дольше всех не запрашивался. В каком-то смысле это алгоритм Белади, но с изменённым направлением времени: вместо будущих запросов изучаются предыдущие. Этот принцип часто оказывается эффективным, поскольку для многих приложений характерна локальность обращений (locality of reference) - программа часто продолжает обращаться к данным, к которым обращалась недавно.