14. Графы. Алгоритмы поиска кратчайших путей

Во взвешенном графе (weighted graph) каждое ребро имеет вес (weight) $w_{e}$. В зависимости от задачи, веса могут быть как целыми, так и вещественными; иногда допускаются отрицательные веса.

Длина (length) пути во взвешенном графе - это сумма весов рёбер на пути. Можно считать, что все рёбра в невзвешенном графе имеют вес, равный единице. Тогда длина пути в невзвешенном графе - это просто количество рёбер в этом пути. Кратчайший путь (shortest path) между двумя вершинами - это путь минимальной длины между этими вершинами (путь с минимальным числом рёбер в невзвешенном случае). Расстояние (distance) между вершинами - длина кратчайшего пути между ними. Если пути между вершинами нет, расстояние считается бесконечным.

Алгоритмы поиска кратчайших путей, которые мы изучим, применимы как для неориентированных, так и для ориентированных графов. Отличие лишь в том, что в ориентированном графе расстояние от вершины $a$ до вершины $b$ может не совпадать с расстоянием от вершины $b$ до вершины $a$.

Поиск в ширину

Поиск в ширину (breadth-first search, BFS) находит расстояния в невзвешенном графе от одной вершины $s$ до всех остальных вершин. Пусть $d_{v}$ - расстояние от $s$ до вершины $v$; $A_{k}$ - множество вершин, расстояние до которых равняется $k: A_{k}=\left\{v \in V: d_{v}=k\right\}$.

Будем находить множества $A_{k}$ последовательно: $A_{0}=\{s\}$; пусть уже найдены $A_{0}, \ldots, A_{k-1}$, тогда $A_{k}$ - это множество вершин из $V \backslash A_{0} \backslash \cdots \backslash A_{k-1}$, в которые ведут рёбра из $A_{k-1}$. Быстро понимать, лежит ли уже вершина $v$ в одном из множеств, можно с помощью массива расстояний dist: $\operatorname{dist}[v]=k$, если $v \in A_{k} ; \operatorname{dist}[v]=\infty$, если множество, в котором лежит $v$, ещё не найдено (или если $v$ не достижима из $s$ ). Здесь $\infty$ - бесконечность; на практике в качестве $\infty$ можно использовать число, заведомо большее, чем длина любого кратчайшего пути; поскольку мы работаем с невзвешенными графами, подойдёт $\infty=|V|$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

vector<vector<int> > A
vector<int> dist(n) # в графе n вершин
fill(dist, inf) # inf - "бесконечность"
dist[s] = 0
A.push_back({s})
for (i = 0; A[i].size() > 0; i += 1):
    A.push_back({})
    for v in A[i]:
        for u in es[v]:
            if dist[u] == inf:
                dist[u] = i + 1
                A[i + 1].push_back(u)

Этот алгоритм уже работает за $O(V+E)$, так как он просматривает список смежности каждой вершины не более одного раза. Можно ещё упростить алгоритм: представим, что множества $A_{0}, A_{1}, \ldots$ хранятся подряд в одном массиве: $q=A_{0} A_{1} A_{2} \ldots$ Тогда вышеописанный алгоритм просматривает элементы этого массива по порядку (то есть по очереди достаёт вершины из начала массива), и иногда добавляет новые вершины в конец массива. Значит, $q$ - это просто очередь; можно не хранить множества $A_{k}$ явно, вместо этого поддерживая очередь $q$. Получившийся алгоритм и называют поиском в ширину.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

vector<int> dist(n) # в графе n вершин
fill(dist, inf)
dist[s] = 0
q <-- s # кладём s в очередь
while not q.empty():
    q --> v # достаём v из очереди
    for u in es[v]:
        if dist[u] == inf:
            dist[u] = dist[v] + 1
            q <-- u

Дерево кратчайших путей

Пока мы научились только находить расстояния от $s$ до остальных вершин. Что делать, если нужно восстановить сами кратчайшие пути? Аналогично дереву поиска в глубину, можно построить дерево поиска в ширину: в него войдут рёбра, при просмотре которых алгоритм добавлял новые вершины в очередь. В простом графе достаточно для каждой вершины $u$ запомнить её предка в дереве поиска в ширину; в графе с кратными рёбрами нужно запомнить, какое именно из кратных рёбер алгоритм просматривал при добавлении u в очередь.

Путь в этом дереве из $s$ в любую вершину $u$ - кратчайший; поэтому дерево поиска в ширину называют также деревом кратчайших путей. Для того, чтобы восстановить кратчайший путь из $s$ в $u$, нужно подниматься по рёбрам дерева из $u$, пока не попадём в $s$.

1
2
3
4

if dist[u] == inf:
    dist[u] = dist[v] + 1
    p[u] = v # v - родитель u в дереве кратчайших путей
    q <-- u

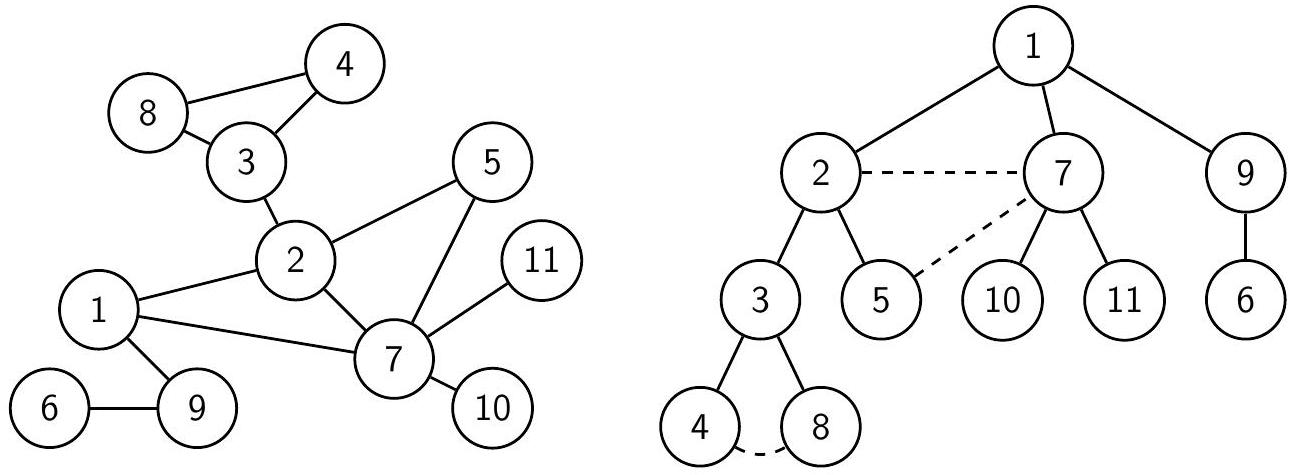
Граф и его дерево кратчайших путей

1
2
3
4
5
6

vector<int> path
while u != s:
    path.push_back(u)
    u = p[u]
path.push_back(s)
reverse(path.begin(), path.end())

0-1-BFS

Пусть теперь каждое ребро в графе имеет вес, равный 0 или 1 . Модифицируем алгоритм поиска в ширину следующим образом: вместо очереди будем использовать дек; при просмотре ребра $e$ из $v$ в $u$ будем класть $u$ в дек, если нашёлся более короткий путь до $u$, чем был известен ранее (если $\operatorname{dist}[u]>\operatorname{dist}[v]+w_{e}$ ). При этом положим $u$ в начало дека, если $w_{e}=0$, и в конец дека, если $w_{e}=1$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

vector<int> dist(n) # в графе n вершин
fill(dist, inf)
dist[s] = 0
deque <-- s # кладём s в дек
while not deque.empty():
    v <-- deque # достаём v из начала дека
    for u, w in es[v]: # u - конец ребра, w - его вес
        if dist[u] > dist[v] + w:
            dist[u] = dist[v] + w
            if w == 0:
                u --> deque # кладём и в начало дека
            else:
                deque <-- u # кладём u в конеп дека

Заметим сначала, что для любой вершины $v$ значение $\operatorname{dist}[v]$ равно $\infty$, либо соответствует длине какого-то пути из $s$ в $v$, поэтому $\operatorname{dist}[v]$ не может оказаться меньше длины кратчайшего пути.

Посмотрим на все вершины в порядке, в котором мы достаём их из дека в первый раз (пока для удобства будем считать, что алгоритм игнорирует повторные попадания вершины в дек). Сначала мы достанем вершину $s$, затем все вершины, достижимые из $s$ только по рёбрам веса 0 . K этому моменту мы достали ровно множество $A_{0}$, при этом в момент извлечения этих вершин из дека расстояние до них уже посчитано корректно.

После этого мы достанем из дека вершины из $V \backslash A_{0}$, достижимые из $A_{0}$ по ребру веса 1 , а также все вершины, достижимые из этих по рёбрам веса 0 , то есть ровно множество $A_{1}$; расстояние до этих вершин также уже посчитано корректно в момент извлечения их из дека. Аналогично, после этого мы достанем множества $A_{2}, A_{3}$, и так далее; в момент извлечения любой вершины из дека расстояние до неё уже посчитано корректно.

Поймём теперь, почему каждая вершина попала в дек не более двух раз (тогда время работы алгоритма оценивается как $O(V+E)$ ). Пусть $u$ попала в дек в первый раз в момент обработки ребра $e=(v, u)$, в $\operatorname{dist}[u]$ при этом было записано $\operatorname{dist}[v]+w_{e}$. K этому моменту уже была хотя бы раз обработана любая вершина $t$ с $d_{t} < d_{v}$. Значит, $d_{u} \geqslant d_{v}$. Тогда, если $w_{e}=0$, то $\operatorname{dist}[u]=d_{u}$, то есть $u$ больше никогда не будет добавлена в дек. Если же $w_{e}=1$, то $\operatorname{dist}[u] \leqslant d_{u}+1$, тогда $u$ может быть добавлена в дек ещё не более одного раза.

$1-k$-BFS

Пусть теперь рёбра в графе могут иметь любой целый вес от 1 до $k$. Как найти кратчайшие пути от $s$ до остальных вершин в таком графе?

Первый способ - заменим каждое ребро длины $l>1$ на $l$ рёбер длины 1 , добавив при этом в граф $l-1$ новую вершину: ребро $e=(u, v), w_{e}=l>1$ заменим на $l$ рёбер $e_{1}=\left(u, a_{1}\right), e_{2}=\left(a_{1}, a_{2}\right), \ldots, e_{l}=\left(a_{l-1}, v\right)$, где $a_{1}, \ldots, a_{l-1}$ - новые вершины (свои для каждого такого ребра). Расстояния между вершинами исходного графа в новом графе не изменились. При этом все рёбра нового графа имеют длину 1 , поэтому расстояния в нём можно найти поиском в ширину. Поскольку в новом графе $O(V+(k-1) E)$ вершин и $O(k E)$ рёбер, получаем время работы $O(V+k E)$.

Второй способ - будем поддерживать свою очередь $q_{i}$ для каждого расстояния $i$. Вначале $q_{0}=\{s\}$, остальные очереди пустые; $\operatorname{dist}[s]=0, \operatorname{dist}[v]=\infty$ для $v \neq s$. Будем рассматривать очереди $q_{i}$ в порядке возрастания $i$. Для каждой вершины $v$ из $q_{i}$ такой, что $\operatorname{dist}[v]=i$, и каждого ребра $e=(v, u)$ такого, что $\operatorname{dist}[u]>\operatorname{dist}[v]+w_{e}$, обновим $\operatorname{dist}[u]$ и положим $u$ в $q_{d i s t[v]+w_{e}}$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

vector<int> dist(n) # в графе n вершин
fill(dist, inf)
dist[s] = 0
q[0] <-- s
for i = 0..((n - 1) * k): # (n - 1) * k - максимально возможное расстояние
    while not q[i].empty():
        v <-- q[i]
        if dist[v] != i:
            continue
        for u, w in es[v]:
            if dist[u] > dist[v] + w:
                dist[u] = dist[v] + w
                q[i + w] <-- u

$\operatorname{dist}[v]$ снова всегда равняется длине какого-то пути от $s$ до $v$ (либо $\infty$ ). Покажем по индукции, что вершины $v$ такие, что $\operatorname{dist}[v]=i$ в момент извлечения $v$ из $q_{i}$ - это ровно вершины множества $A_{i}$. Это верно для $i=0$; для $i>0$ в $q_{i}$ попадают вершины из $V \backslash A_{0} \backslash \cdots \backslash A_{i-1}$, в которые ведёт ребро веса 1 из $A_{i-1}$, веса 2 из $A_{i-2}, \ldots$ или веса $k$ из $A_{i-k}$ (то есть вершины множества $A_{i}$ ), а также, возможно, часть вершин из $A_{0} \cup \cdots \cup A_{i-1}$, в которые ведут такие же рёбра. Тогда такие вершины $v$, что $\operatorname{dist}[v]=i$ в момент извлечения $v$ из $q_{i}$ - это ровно вершины множества $A_{i}$.

При этом каждая вершина попадёт в не более чем $k$ различных очередей: пусть вершина $u$ попала в $q_{d i s t[v]+w_{e}}$ при рассмотрении ребра $e=(v, u)$, до этого было верно $\operatorname{dist}[u]=\infty$. Тогда в этот момент $\operatorname{dist}[v]=d_{v}$, откуда $d_{u}>d_{v}$ (иначе $u$ уже попала бы до этого в очередь $q_{i}$ для $i \leqslant d_{v}$ ). Но тогда $\operatorname{dist}[u]=\operatorname{dist}[v]+w_{e}

Получаем время работы $O(k V+E)$, так как каждая вершина попала не более, чем в $k$ очередей; при этом список смежности каждой вершины был рассмотрен ровно один раз.

Произвольные веса

Что делать, если веса рёбер - произвольные вещественные числа? Попробуем модифицировать алгоритм поиска в ширину так, чтобы он всё ещё работал. Первая идея: будем класть вершину $v$ в очередь каждый раз, когда значение $\operatorname{dist}[v]$ уменьшается; теперь каждую вершину, мы, возможно, будем обрабатывать несколько раз. Другая идея: вместо обычной очереди будем пользоваться очередью с приоритетами, извлекая на каждом шаге такую вершину $v$, что значение $\operatorname{dist}[v]$ минимально среди всех вершин в очереди.

Обе эти идеи при правильной реализации приводят к рабочим алгоритмам: первая — к алгоритму Форда-Беллмана, вторая - к алгоритму Дейкстры. Изучением этих алгоритмов мы сейчас и займёмся.

Алгоритм Дейкстры

Алгоритм Дейкстры (Dijkstra, 1959) находит расстояния от вершины $s$ до всех остальных вершин в графе с неотрицательными весами рёбер. Алгоритм постепенно расширяет множество $A$ вершин, до которых уже найдены расстояния и кратчайшие пути. При этом для любой вершины $v$ алгоритм поддерживает значение $\operatorname{dist}[v]$, равное $\infty$ либо длине какого-то пути из $s$ в $v$.

Как и раньше, за $d_{v}$ будем обозначать длину кратчайшего пути от $s$ до $v$. Вначале $\operatorname{dist}[s]=0, \operatorname{dist}[v]=\infty$ для $v \neq s$, множество $A$ пусто. На каждом шаге алгоритм добавляет в множество $A$ вершину $v$ с минимальным значением $\operatorname{dist}[v]$ среди всех вершин из $V \backslash A$ (на первом шаге в $A$ всегда добавляется вершина $s$ ). После этого алгоритм просматривает все исходящие из только что добавленной вершины $v$ рёбра, и для каждого ребра $e=(v, u)$ обновляет значение $\operatorname{dist}[u]$ значением $\min \left(\operatorname{dist}[u], \operatorname{dist}[v]+w_{e}\right)$; будем называть эту операцию релаксацией ребра $e$.

Докажем по индукции, что в момент добавления вершины $v$ в множество $A$ расстояние от $s$ до $v$ уже найдено: $\operatorname{dist}[v]=d_{v}$. Это верно на первом шаге алгоритма, когда в $A$ добавляется сама вершина $s$. Далее, пусть для всех вершин из $A$ расстояние до них уже найдено, $\operatorname{dist}[v]=\min _{u \in V \backslash A} \operatorname{dist}[u]$; нужно показать, что $\operatorname{dist}[v]=d_{v}$.

Пусть $P$ - кратчайший путь из $s$ в $v$; здесь и дальше длину пути $P$ будем обозначать как $l(P)$. Пусть $u$ - первая вершина на пути $P$, не лежащая в множестве $A ; x$ - вершина на пути перед ней, $e=(x, u)$ - соединяющее их ребро. Обозначим часть пути от $s$ до $x$ за $P_{1}$, часть пути от $u$ до $v$ за $P_{2}$, тогда $l(P)=l\left(P_{1}\right)+w_{e}+l\left(P_{2}\right) \geqslant l\left(P_{1}\right)+w_{e}$ (так как веса рёбер неотрицательны, то есть $\left.l\left(P_{2}\right) \geqslant 0\right)$. $l\left(P_{1}\right) \geqslant d_{x}$, при этом $d_{x}=\operatorname{dist}[x]$ по предположению индукции (так как $x \in A$ ). Кроме того, $\operatorname{dist}[u] \leqslant \operatorname{dist}[x]+w_{e}$, так как при добавлении $x$ в $A$ была произведена релаксация ребра $e$. Соберём все неравенства вместе:

С другой стороны, $\operatorname{dist}[v] \geqslant d_{v}$, поскольку $\operatorname{dist}[v]$ равно $\infty$ или соответствует длине какого-то пути из $s$ в $v$.

Реализация

Удобно воспользоваться очередью с приоритетами: будем хранить в очереди ещё не рассмотренные вершины с приоритетами, равными значениям dist. Тогда в ходе алгоритма нужно $O(V)$ раз извлечь из очереди вершину с минимальным приоритетом, и $O(E)$ раз уменьшить приоритет вершины в очереди.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

vector<int> dist(n) # в графе n вершин
fill(dist, inf)
dist[s] = 0
for v = 0..(n - 1):
    q <-- (v, dist[v]) # кладём в очередь вершину v с приоритетом dist[v]
for i = 0..(n - 1):
    v <-- q # достаём из очереди вершину с минимальным приоритетом
    for u, w in es[v]:
        if dist[u] > dist[v] + w:
            dist[u] = dist[v] + w
            q.decreaseKey(u, dist[u]) # уменьшаем значение приоритета u до dist[u]

Очередь с приоритетами можно реализовывать разными способами: можно просто хранить значения dist в массиве, и искать минимум проходом по массиву за $O(V)$ (дополнительно надо хранить пометки о том, была ли вершина уже рассмотрена). В этом случае время работы алгоритма составит $O(V \cdot V+E \cdot 1)=O\left(V^{2}+E\right)$.

Если реализовать очередь с приоритетами с помощью двоичной кучи, то получим время работы $O(V \cdot \log V+E \cdot \log V)=O((V+E) \log V)$.

Первый способ эффективнее в случае плотного графа ( $E=\Omega\left(V^{2}\right)$ ), второй - при $E=o\left(V^{2}\right)$. (R) При реализации очереди с приоритетами при помощи фибоначчиевой кучи получается теоретическая оценка времени работы $O(V \log V+E)$, так как амортизированное время выполнения операции уменьшения приоритета в таких кучах равно $O(1)$. Если известно, что веса рёбер и длины путей - целые числа, не превосходящие $C$, реализация очереди с приоритетами с помощью дерева Ван-Эмде-Боаса даст оценку времени работы $O((V+E) \log \log C)$.

Восстановление кратчайшего пути

Восстановление кратчайшего пути осуществляется полностью аналогично тому, как это делалось в алгоритме поиска в ширину: запомним для каждой вершины $v$ последнее ребро, при релаксации которого $\operatorname{dist}[v]$ уменьшилось. Эти рёбра снова образуют дерево кратчайших путей, поднимаясь по ним, можно восстановить кратчайший путь от $s$ до любой вершины $v$ за время, пропорциональное количеству рёбер на этом пути.

Алгоритм $A^{*}$

Алгоритм $A^{*}$ (произносится как “A-star”; Hart, Nilsson, Raphael, 1968) находит расстояния от вершины $s$ до вершины $t$ в графе с неотрицательными весами рёбер. В каком-то смысле он является модификацией алгоритма Дейкстры, более эффективной в случае, когда нужно найти расстояние от $s$ лишь до одной вершины $t$, а не до всех остальных вершин.

Алгоритм использует вспомогательные значения $f[v]$ для каждой вершины графа $v$. $f$ - какая-то дополнительная информация о графе. Обычно (хотя не всегда) под $f[v]$ имеется в виду какая-то оценка снизу на расстояние от $v$ до $t$ в графе. Например, пусть вершины графа - это точки на плоскости, а вес ребра - расстояние на плоскости между концами этого ребра. Тогда в качестве $f[v]$ логично взять расстояние на плоскости между $v$ и $t$ : для любого пути в графе из $v$ в $t$ длина этого пути будет не меньше $f[v]$.

Единственное отличие алгоритма $A^{*}$ от алгоритма Дейкстры: в качестве приоритета вершины $v$ используется не $\operatorname{dist}[v]$, а $\operatorname{dist}[v]+f[v]$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

vector<int> dist(n) # в графе n вершин
fill(dist, inf)
dist[s] = 0
for v = 0..(n - 1):
    q<-- (v, dist[v] + f[v])
for i = 0..(n - 1):
    v <-- q
    if v == t:
        break # нас интересовало только расстояние до t
    for u, w in es[v]:
        if dist[u] > dist[v] + w:
            dist[u] = dist[v] + w
            q.decreaseKey(u, dist[u] + f[u])

Интуитивно это можно понимать так: алгоритм пытается в первую очередь рассматривать вершины, которые больше похожи на лежащие на кратчайшем пути от $s$ к $t$. Поскольку $d i s t[v]+f[v]$ - это оценка на длину пути из $s$ в $t$, проходящего через $v$, логично сначала рассматривать вершины, для которых эта величина минимальна.

Неравенство треугольника

Будем говорить, что для $f$ выполняется неравенство треугольника, если $f[a] \leqslant f[b]+w_{e}$ для любого ребра $e$ из $a$ в $b$. В примере выше $f$ удовлетворяет неравенству треугольника, поскольку оно эквивалентно неравенству треугольника для расстояний между точками на плоскости (нужно рассмотреть треугольник на вершинах $a, b, t$ ).

Алгоритм $A^{*}$ останавливается, когда находит расстояние до вершины $t$. Такое же условие остановки можно добавить в алгоритм Дейкстры, если расстояние до остальных вершин нас не интересует; будем называть такую версию алгоритмом Дейкстры с break.

Заметим, что если $f$ удовлетворяет условию последнего предложения, то $f[v]$ является оценкой снизу на расстояние от $v$ до $t$ : пусть кратчайший путь $P$ из $v$ в $t$ состоит из рёбер $e_{1}, \ldots, e_{k}$. Тогда, применив несколько раз неравенство треугольника, получаем

поскольку $f[t]=0$.

Алгоритм Форда-Беллмана

Алгоритм Форда-Беллмана (Shimbel, 1955; Bellman, 1958; Ford, 1956; Moore, 1957) находит расстояние от вершины $s$ до всех остальных вершин в графе с произвольными вещественными весами, но без отрицательных циклов (циклов, длина которых отрицательна).

Если из $s$ достижим отрицательный цикл, то кратчайшего пути до любой вершины на этом цикле (и до любой вершины, достижимой из вершин цикла) не существует: к любому пути можно добавлять проходы по циклу, при этом с каждым таким проходом длина пути будет уменьшаться.

✍️ Заметим, что в неориентированном графе любое ребро отрицательного веса соответствует отрицательному циклу, который получается при проходе по этому ребру вперёд и назад. Поэтому в неориентированных графах понятие кратчайшего пути имеет смысл, только если веса всех рёбер неотрицательны.

Пусть в графе нет (достижимых из $s$ ) отрицательных циклов. Тогда для любой достижимой из $s$ вершины $v$ найдётся простой (без повторяющихся вершин) кратчайший путь из $s$ в $v$. Если бы это было не так, то путь содержал бы цикл. Тогда, удалив цикл из пути, мы не увеличим длину пути. Значит, достаточно искать простые кратчайшие пути из $s$ в другие вершины. С этой задачей справляется следующий алгоритм:

1
2
3
4
5
6

fill(dist, inf)
dist[s] = 0
for k = 0..(n - 2):
    for v = 0..(n - 1):
        for u, w in es[v]:
            dist[u] = min(dist[u], dist[v] + w)

Всё, что делает этот алгоритм — $|V|-1$ раз проводит релаксацию всех рёбер графа. Почему он найдёт расстояния до всех вершин корректно? Пусть $Q$ - любой простой путь из $s$ в $v$; пусть он состоит из рёбер $e_{1}, \ldots, e_{k}, k \leqslant|V|-1$. На первом шаге внешнего цикла алгоритм проведёт релаксацию ребра $e_{1}$, на втором шаге - ребра $e_{2}, \ldots$, на $k$-м - ребра $e_{k}$. Тогда после $k$ шагов внешнего цикла

Мы знаем, что если $v$ достижима из $s$, то существует простой кратчайший путь $P$ из $s$ в $v$, тогда после $|V|-1$ шага внешнего цикла $\operatorname{dist}[v] \leqslant l(P)$. С другой стороны, $\operatorname{dist}[v]$ в любой момент - либо $\infty$, либо длина какого-то пути из $s$ в $v$. Значит, $\operatorname{dist}[v] \geqslant l(P)$.

Время работы алгоритма — $O(V E)$.

Восстановление кратчайшего пути

Восстановление кратчайшего пути полностью аналогично алгоритмам поиска в ширину и Дейкстры - запоминаем для каждой вершины последнее ребро, при релаксации которого $\operatorname{dist}[v]$ уменьшилось; эти рёбра образуют дерево кратчайших путей и позволяют восстановить кратчайший путь от $s$ до любой достижимой из неё вершины $v$ за время, пропорциональное количеству рёбер на этом пути.

Поиск отрицательного цикла

Что делать, если неизвестно, есть ли в графе отрицательные циклы? С помощью алгоритма Форда-Беллмана можно проверить их наличие, и даже найти один из отрицательных циклов, если они есть. Всё, что нужно сделать - ещё одну ( $|V|$-ю по счёту) релаксацию всех

рёбер графа в конце алгоритма. Будем называть релаксацию ребра $e=(v, u)$ успешной, если в результате её выполнения $\operatorname{dist}[u]$ строго уменьшилось.

Если в графе нет отрицательных циклов, то успешных релаксаций на дополнительном шаге алгоритма не произойдёт, поскольку после $|V|-1$ шага все расстояния уже были найдены. С другой стороны, пусть в графе есть достижимый из $s$ отрицательный цикл, состоящий из вершин $v_{1}, \ldots, v_{k}$ и рёбер $e_{1}, \ldots, e_{k}$ ( $e_{i}$ соединяет $v_{i}$ и $v_{i+1}, v_{k+1}=v_{1}$ ). Тогда, если на последнем шаге алгоритма не было успешных релаксаций, то $dist \left[v_{i+1}\right] \leqslant\operatorname{dist}\left[v_{i}\right]+w_{e_{i}}$ для $1 \leqslant i \leqslant k$, откуда

то есть $w_{e_{1}}+\cdots+w_{e_{k}} \geqslant 0$, что противоречит отрицательности цикла. Итак, для того, чтобы проверить, если ли в графе достижимые из $s$ отрицательные циклы, достаточно проверить, произойдёт ли на дополнительном шаге алгоритма хотя бы одна успешная релаксация.

✍️ Для того, чтобы проверить, есть ли вообще в графе отрицательные циклы (не обязательно достижимые из какой-то фиксированной вершины графа), можно добавить в граф новую вершину, провести из неё во все остальные вершины рёбра веса 0 , и использовать эту вершину в качестве $s$.

Восстановить отрицательный цикл можно примерно так же, как восстанавливается кратчайший путь: пусть $e[v]$ - последнее ребро, при релаксации которого $\operatorname{dist}[v]$ уменьшилось, $p[v]$ - его второй конец. $p[v]$ и $e[v]$ не определены, если $\operatorname{dist}[v]$ ни разу не уменьшалось в ходе алгоритма.

Почему описанный выше алгоритм действительно найдёт отрицательный цикл? Сначала нужно понять, почему последовательность действительно зациклится. Предположим, что повтора вершины так и не произошло. Переобозначим выписанную последовательность за $v=v_{1}, u=v_{2}, \ldots, v_{k}$. Тогда $p\left[v_{k}\right]$ не определено, при этом $\operatorname{dist}\left[v_{k}\right] \neq \infty$, поскольку $v_{k}$ участвовала в успешной релаксации ребра $e\left[v_{k-1}\right]$. Тогда $v_{k}=s, \operatorname{dist}\left[v_{k}\right]=0$. Значит, выписанная последовательность образует простой путь $P$ из $s$ в $v$. При этом по лемме выполняется неравенство

С другой стороны, поскольку $P$ - простой путь, $\operatorname{dist}[v] \leqslant l(P)$ после $|V|-1$ шага внешнего цикла. Но это противоречит тому, что $\operatorname{dist}[v]$ уменьшилось при релаксации ребра $e[v]$ на дополнительном шаге алгоритма.

Итак, последовательность зациклилась; обозначим вершины в подотрезке последовательности за $v_{1}, \ldots, v_{k}, v_{k+1}=v_{1}\left(p\left[v_{i}\right]=v_{i+1}\right)$; эти вершины вместе с рёбрами $e\left[v_{1}\right], \ldots, e\left[v_{k}\right]$ образуют цикл $C$. Осталось показать, что длина этого цикла отрицательна. По лемме, $\operatorname{dist}\left[v_{i}\right] \geqslant \operatorname{dist}\left[v_{i+1}\right]+w_{e\left[v_{i}\right]}$. Просуммируем эти неравенства по $i$ от 1 до $k$ и получим

откуда $l(C)=w_{e\left[v_{1}\right]}+\cdots+w_{e\left[v_{k}\right]} \leqslant 0$. Нам же нужно показать, что $l(C) < 0$. Пусть $v_{j}-$ вершина на цикле $C$, значение $\operatorname{dist}\left[v_{j}\right]$ которой менялось в последний раз позже остальных вершин на цикле. Тогда $\operatorname{dist}\left[v_{j-1}\right]>\operatorname{dist}\left[v_{j}\right]+w_{e\left[v_{j-1}\right]}$, поскольку $\operatorname{dist}\left[v_{j}\right]$ уменьшилось после релаксации ребра $e\left[v_{j-1}\right]$. Значит, одно из $k$ неравенств выше строгое, и $l(C) < 0$.

Алгоритм Форда-Беллмана с очередью

Вернёмся к графам без отрицательных циклов. Алгоритм Форда-Беллмана можно соптимизировать, избавившись от повторного выполнения одних и тех же действий. При этом получается алгоритм, который называют алгоритмом Форда-Беллмана с очередью; также он известен как SPFA (Shortest path faster algorithm; Moore, 1959). Он имеет ту же теоретическую оценку времени, что и алгоритм Форда-Беллмана, но на практике часто работает намного быстрее.

Первая идея - на $k$-м шаге алгоритма нет смысла проводить релаксацию исходящих из $v$ рёбер, если $\operatorname{dist}[v]$ не поменялось с $(k-1)$-го шага. Обозначим за $B_{k}$ множество таких вершин $v$, что dist $[v]$ уменьшилось в течение ( $k-1$ )-го шага; $B_{0}=\{s\}$. На $k$-м шаге алгоритма достаточно произвести релаксацию рёбер, исходящих из вершин множества $B_{k}$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

fill(dist, inf)
dist[s] = 0
B[0] <-- s
for k = 0..(n - 2):
    for v in B[k]:
        for u, w in es[v]:
            if dist[u] > dist[v] + w:
                dist[u] = dist[v] + w
                if u not in B[k + 1]:
                    B[k+1] <-- u

Получившийся алгоритм очень похож на версию алгоритма поиска в ширину, в которой множества $A_{k}=\left\{v \in V: d_{v}=k\right\}$ строились явно. Как и в том случае, множества $B_{k}$ можно моделировать с помощью очереди: будем складывать вершину $v$ в очередь, если $d i s t[v]$ уменьшилось, и $v$ в данный момент ещё не лежит в очереди. Такой алгоритм с очередью эквивалентен предыдущему алгоритму, но с ещё одной оптимизацией: теперь мы не будем класть вершину $v$ в $B_{k+1}$, если с момента её обработки в $B_{k}$ до конца обработки вершин из $B_{k} \operatorname{dist}[v]$ не менялось. Эту оптимизацию можно сделать, так как релаксация рёбер, исходящих из такой вершины $v$, на ( $k+1$ )-м шаге бессмысленна, поскольку значение dist $[v]$ не поменялось с предыдущей релаксации тех же рёбер.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

fill(dist, inf)
fill(inQueue, False)
dist[s] = 0
q <-- s, inQueue[s] = True
while not q.empty():
    q --> v, inQueue[v] = False
    for u, w in es[v]:
        if dist[u] > dist[v] + w:
            dist[u] = dist[v] + w
            if not inQueue[u]:
            q <-- u, inQueue[u] = True

Время работы получившегося алгоритма можно оценить как $O(V E)$, поскольку он делает не больше релаксаций рёбер, чем делал обычный алгоритм Форда-Беллмана.

Алгоритм Флойда

Алгоритм Флойда (Floyd, 1962; Roy, 1959; Warshall, 1962) находит расстояния между всеми парами вершин в графе с произвольными вещественными весами, но без отрицательных циклов.

Алгоритм последовательно для $0 \leqslant k \leqslant n$ и для каждой пары вершин $0 \leqslant i, j < n$ вычисляет $\operatorname{dist}[k, i, j]$ - минимальную длину пути из $i$ в $j$, промежуточные вершины (все вершины, кроме концов пути) в котором имеют номера меньше $k$. Будем считать, что $\operatorname{dist}[k, i, j]=\infty$, если ни одного такого пути не существует. $\operatorname{dist}[n, i, j]$ - это расстояние от $i$ до $j$.

Если $i \neq j$, то $\operatorname{dist}[0, i, j]=w_{e}$, где $e-$ минимальное по весу ребро из $i$ в $j$; $\operatorname{dist}[0, i, j]=\infty$, если из $i$ в $j$ нет рёбер. $\operatorname{dist}[0, i, i]=0$ для любого $i$.

Пусть теперь $k \geqslant 0$, для всех пар вершин $i, j$ уже известно dist $[k, i, j]$; чему равняется $\operatorname{dist}[k+1, i, j]$ ? Пусть $P$ - минимальный по длине путь из $i$ в $j$, промежуточные вершины в котором имеют номера меньше $k+1$. Если вершина $k$ не является промежуточной вершиной $P$, то $\operatorname{dist}[k+1, i, j]=\operatorname{dist}[k, i, j]$. Если же $k$ является промежуточной вершиной $P$, то можно считать, что $P$ проходит через $k$ ровно один раз (так как в графе нет отрицательных циклов). Тогда $P$ распадается на два пути: путь $P_{1}$ из $i$ в $k$, и путь $P_{2}$ из $k$ в $j$. При этом промежуточные вершины в путях $P_{1}, P_{2}$ имеют номера меньше $k ; P_{1}, P_{2}$ имеют минимально возможную длину среди таких путей (иначе $P$ был бы не минимальным по длине). Значит, $l\left(P_{1}\right)=\operatorname{dist}[k, i, k], l\left(P_{2}\right)=\operatorname{dist}[k, k, j]$. Итак,

Получаем алгоритм со временем работы $O\left(V^{3}\right)$, использующий $O\left(V^{3}\right)$ дополнительной памяти. На самом деле можно ограничиться $O\left(V^{2}\right)$ памяти: для любого $k$ будем использовать одно и то же $\operatorname{dist}[i, j]$ вместо $\operatorname{dist}[k, i, j]$.

1
2
3
4
5
6

# dist[i, j] равняется минимальному весу ребра из i в j или inf, если рёбер из i в ј нет
# dist[i, i] = 0
for k = 0..(n - 1):
    for i = 0..(n - 1):
        for j = 0..(n - 1):
            dist[i, j] = min(dist[i, j], dist[i, k] + dist[k, j])

Почему алгоритм с двумерным массивом вместо трёхмерного остаётся корректным? В любой момент $\operatorname{dist}[i, j]$ - это длина какого-то пути из $i$ в $j$; при этом после $k$ итераций внешнего цикла $\operatorname{dist}[i, j]$ не больше длины любого пути из $i$ в $j$, промежуточные вершины в котором имеют номера меньше $k$ (это было верно для $\operatorname{dist}[k, i, j]$, a $\operatorname{dist}[i, j] \leqslant \operatorname{dist}[k, i, j]$ после $k$ итераций). Значит, после $n$ итераций $\operatorname{dist}[i, j]$ - это расстояние от $i$ до $j$.

Восстановление пути

Для каждой пары $i, j$ запомним $\operatorname{maxNum}[i, j]$ - последнее $k$, при котором $\operatorname{dist}[i, j]$ уменьшилось. Тогда $\operatorname{maxN} \operatorname{Num}[i, j]$ - максимальная по номеру вершина на кратчайшем пути из $i$ в $j$; кратчайший путь из $i$ в $j$ состоит из двух путей: кратчайшего пути из $i$ в $k$ и из $k$ в $j$. Каждый из этих путей восстановим рекурсивно теми же рассуждениями.

Альтернативный способ: для каждой пары $i, j$ запомним first $[i, j]$ - первую после $i$ вершину на кратчайшем пути. Вначале $\operatorname{first}[i, j]=j$, если $\operatorname{dist}[i, j]$ равняется весу ребра из $i$ в $j$, и -1 , если рёбер из $i$ в $j$ нет. В момент, когда $\operatorname{dist}[i, j]$ обновляется значением $\operatorname{dist}[i, k]+\operatorname{dist}[k, j]$, обновим $\operatorname{first}[i, j]$ значением $\operatorname{first}[i, k]$. Теперь для того, чтобы восстановить путь из $i$ в $j$, надо заменять $i$ на $\operatorname{first}[i, j]$, пока $i$ не станет равно $j$.

Графы с отрицательными циклами

Что делать, если в графе могут быть отрицательные циклы? Заметим, что массив $\operatorname{dist}$, получившийся в результате выполнения алгоритма, удовлетворяет следующим утверждениям:

• Вершина $i$ лежит на отрицательном цикле тогда и только тогда, когда $\operatorname{dist}[i, i]<0$.

Действительно, поскольку $\operatorname{dist}[i, i]$ - это длина какого-то пути из $i$ в $i$, если $\operatorname{dist}[i, i]<0$, то $i$ лежит на отрицательном цикле. С другой стороны, пусть $i$ лежит на отрицательном цикле $C$, и $k$ - вершина с максимальным номером на этом цикле, не считая $i$. Тогда после $k$-го шага алгоритма $\operatorname{dist}[i, i] \leqslant \operatorname{dist}[i, k]+\operatorname{dist}[k, i] \leqslant l(C)<0$.

• В графе не существует кратчайшего пути из $a$ в $b$ тогда и только тогда, когда существует такая вершина $i$, что $\operatorname{dist}[i, i]<0, \operatorname{dist}[a, i]<\infty, \operatorname{dist}[i, b]<\infty$.

Действительно, в графе не существует кратчайшего пути из $a$ в $b$ тогда и только тогда, когда из а достижим отрицательный цикл, из которого достижима вершина $b$; вершина $i$ из условия выше - любая вершина на этом цикле.

Заметим, что, пользуясь первым утверждением, можно не только понять, есть ли в графе отрицательные циклы, но и восстановить какой-то из них: это делается так же, как восстанавливается кратчайший путь в графе без отрицательных циклов.

Пользуясь вторым утверждением, можно за $O\left(V^{3}\right)$ для каждой пары вершин $a, b$ понять, существует ли кратчайший путь из $a$ в $b$. Если путь существует, то его длина была найдена алгоритмом корректно, и путь может быть восстановлен обычным способом.

✍️ В графе с неотрицательными весами рёбер расстояния между всеми парами вершин можно найти несколькими запусками алгоритма Дейкстры за $O\left(V^{2} \log V+V E\right)$ (если использовать фибоначчиеву кучу). В разреженных графах ( $E=o\left(V^{2}\right)$ ) этот способ даёт лучшую теоретическую оценку, чем алгоритм Флойда. В графах с произвольными вещественными весами рёбер, но без отрицательных циклов, можно добиться той же оценки времени работы, специальным образом модифицировав веса рёбер (Johnson, 1977). Мы изучим эту идею подробно, когда будем изучать задачу поиска максимального потока минимальной стоимости.

✍️ В неориентированном графе с неотрицательными весами рёбер расстояния от одной вершины до всех остальных можно находить за $O(V+E)$ (Thorup, 1999). Несколькими запусками этого алгоритма можно найти расстояния между всеми парами вершин за $O\left(V^{2}+V E\right)$.